题目内容
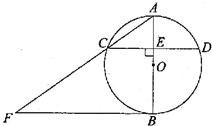
如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为 的中点.
的中点.

(1)求证:OF∥BD;
(2)若 ,且⊙O的半径R=6cm.①求证:点F为线段OC的中点; ②求图中阴影部分(弓形)的面积.
,且⊙O的半径R=6cm.①求证:点F为线段OC的中点; ②求图中阴影部分(弓形)的面积.
 的中点.
的中点.
(1)求证:OF∥BD;
(2)若
 ,且⊙O的半径R=6cm.①求证:点F为线段OC的中点; ②求图中阴影部分(弓形)的面积.
,且⊙O的半径R=6cm.①求证:点F为线段OC的中点; ②求图中阴影部分(弓形)的面积.(1)证明见解析(2)①证明见解析② cm2
cm2
 cm2
cm2(1)证明:∵OC为半径,点C为 的中点,∴OC⊥AD。
的中点,∴OC⊥AD。
∵AB为直径,∴∠BDA=90°,BD⊥AD。∴OF∥BD。
(2)①证明:∵点O为AB的中点,点F为AD的中点,∴OF= BD。
BD。
∵FC∥BD,∴∠FCE=∠DBE。
∵∠FEC=∠DEB,∴△ECF∽△EBD,
∴ ,∴FC=
,∴FC= BD。
BD。
∴FC=FO,即点F为线段OC的中点。
②解:∵FC=FO,OC⊥AD,∴AC=AO,
又∵AO=CO,∴△AOC为等边三角形。
∴根据锐角三角函数定义,得△AOC的高为 。
。
∴ (cm2)。
(cm2)。
答:图中阴影部分(弓形)的面积为 cm2。
cm2。
(1)由垂径定理可知OC⊥AD,由圆周角定理可知BD⊥AD,从而证明OF∥BD。
(2)①由OF∥BD可证△ECF∽△EBD,利用相似比证明BD=2CF,再证OF为△ABD的中位线,得出BD=2OF,即CF=OF,证明点F为线段OC的中点;
②根据S阴=S扇形AOC﹣S△AOC,求面积。
 的中点,∴OC⊥AD。
的中点,∴OC⊥AD。∵AB为直径,∴∠BDA=90°,BD⊥AD。∴OF∥BD。
(2)①证明:∵点O为AB的中点,点F为AD的中点,∴OF=
 BD。
BD。∵FC∥BD,∴∠FCE=∠DBE。
∵∠FEC=∠DEB,∴△ECF∽△EBD,
∴
 ,∴FC=
,∴FC= BD。
BD。∴FC=FO,即点F为线段OC的中点。
②解:∵FC=FO,OC⊥AD,∴AC=AO,
又∵AO=CO,∴△AOC为等边三角形。
∴根据锐角三角函数定义,得△AOC的高为
 。
。∴
 (cm2)。
(cm2)。答:图中阴影部分(弓形)的面积为
 cm2。
cm2。(1)由垂径定理可知OC⊥AD,由圆周角定理可知BD⊥AD,从而证明OF∥BD。
(2)①由OF∥BD可证△ECF∽△EBD,利用相似比证明BD=2CF,再证OF为△ABD的中位线,得出BD=2OF,即CF=OF,证明点F为线段OC的中点;
②根据S阴=S扇形AOC﹣S△AOC,求面积。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目