题目内容
如图,二次函数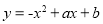 的图象与
的图象与 轴交于
轴交于 ,
, 两点,且与y轴交于点C.
两点,且与y轴交于点C.

(1)求该抛物线的关系式,并判断 的形状;
的形状;
(2)在x轴上方的抛物线上有一点D,且以A、B、C、D四点为顶点的四边形是等腰梯形,请直接写出D点的坐标 ;
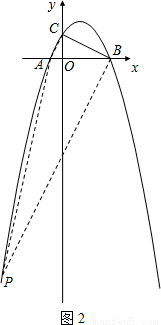
(3)在此抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形是直角梯形?若存在,求出P点的坐标;若不存在,说明理由。
(1)抛物线的解析式为y=-x2+ x+1;△ABC是直角三角形,且∠ACB=90°(2)D(
x+1;△ABC是直角三角形,且∠ACB=90°(2)D( ,1);(3)点P(
,1);(3)点P( ,-
,- )或(-
)或(- ,-9)
,-9)
【解析】
试题分析:(1)将A、B的坐标代入抛物线的解析式中即可确定抛物线的解析式;进而可得到C点坐标,进而可求出AC、BC、AB的长,然后再判断△ABC的形状;
(2)根据抛物线和等腰梯形的对称性知,点C关于抛物线对称轴的对称点符合点D的要求,由此可求出点D的坐标;
(3)在(1)题已将证得∠ACB=90°,若A、C、B、P四点为顶点的四边形是直角梯形,则有两种情况需要考虑:
①以BC、AP为底,AC为高;可先求出直线BC的解析式,进而可确定直线AP的解析式,联立抛物线的解析式即可求出点P的坐标.
②以AC、BP为底,BC为高;方法同①.
试题解析:(1)由题意得: ,
,
解得 ;
;
∴抛物线的解析式为y=-x2+ x+1;
x+1;
∴C(0,1);
∴AC2= +1=
+1= ,BC2=1+4=5,AB2=(2+
,BC2=1+4=5,AB2=(2+ )2=
)2= ;
;
∴AC2+BC2=AB2,即△ABC是直角三角形,且∠ACB=90°
(2)由(1)的抛物线知:其对称轴方程为x= ;
;
根据抛物线和等腰梯形的对称性知:点D( ,1);
,1);

(3)存在,点P( ,-
,- )或(-
)或(- ,-9);
,-9);
若以A、C、B、P四点为顶点的直角梯形以BC、AP为底;
∵B(2,0),C(0,1),
∴直线BC的解析式为:y=- x+1;
x+1;
设过点A且平行于BC的直线的解析式为y=- x+h,
x+h,
则有:(- )×(-
)×(- )+h=0,h=-
)+h=0,h=- ;
;
∴y=- x-
x- ;
;
联立抛物线的解析式有:

解得: 或
或
∴点P( ,
, );
);
若以A、C、B、P四点为顶点的直角梯形以AC、BP为底,
同理可求得P(- ,-9);
,-9);
故当P( ,
, )或(-
)或(- ,-9);时,以A、C、B、P四点为顶点的四边形是直角梯形.
,-9);时,以A、C、B、P四点为顶点的四边形是直角梯形.
(根据抛物线的对称性求出另一个P点坐标亦可)
考点:二次函数综合题.

 阅读快车系列答案
阅读快车系列答案如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC= ( )
| A.2:5 | B.2:3 | C.3:5 | D.3:2 |
 与y轴的交点为(0,
与y轴的交点为(0, )则该抛物线与x轴的交点是( )
)则该抛物线与x轴的交点是( )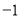 ,0)和(0,3) B.(0,
,0)和(0,3) B.(0,
 的图象,取自变量x的5个值,请你指出这个算错的y值所对应的x= 。
的图象,取自变量x的5个值,请你指出这个算错的y值所对应的x= 。 
