题目内容
 (重点题)在?ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,∠AEF=54°,则∠B=
(重点题)在?ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,∠AEF=54°,则∠B=分析:过F作AB、CD的平行线FG,由于F是AD的中点,那么G是BC的中点,即Rt△BCE斜边上的中点,由此可得BC=2EG=2FG,即△GEF、△BEG都是等腰三角形,因此求∠B的度数,只需求得∠BEG的度数即可;易知四边形ABGF是平行四边形,得∠EFG=∠AEF,由此可求得∠FEG的度数,即可得到∠AEG的度数,根据邻补角的定义可得∠BEG的值,由此得解.
解答: 解:过F作FG∥AB∥CD,交BC于G;
解:过F作FG∥AB∥CD,交BC于G;
则四边形ABGF是平行四边形,所以AF=BG,即G是BC的中点;
∵BC=2AB,为AD的中点,
∴BG=AB=FG=AF,
连接EG,在Rt△BEC中,EG是斜边上的中线,则BG=GE=FG=
BC;
∵AE∥FG,∴∠EFG=∠AEF=∠FEG=54°,
∴∠AEG=∠AEF+∠FEG=108°,
∴∠B=∠BEG=180°-108°=72°.
故答案为:72°.
 解:过F作FG∥AB∥CD,交BC于G;
解:过F作FG∥AB∥CD,交BC于G;则四边形ABGF是平行四边形,所以AF=BG,即G是BC的中点;
∵BC=2AB,为AD的中点,
∴BG=AB=FG=AF,
连接EG,在Rt△BEC中,EG是斜边上的中线,则BG=GE=FG=
| 1 |
| 2 |
∵AE∥FG,∴∠EFG=∠AEF=∠FEG=54°,
∴∠AEG=∠AEF+∠FEG=108°,
∴∠B=∠BEG=180°-108°=72°.
故答案为:72°.
点评:此题主要考查了平行四边形的性质、直角三角形的性质以及等腰三角形的判定和性质,正确地构造出与所求相关的等腰三角形是解决问题的关键.

练习册系列答案
相关题目
 3、如图,在?ABCD中,对角线AC,BD交于点O,EF是过点O的一条直线,交AB于点E,交DC于点F.则OE与OF有什么数量关系?答
3、如图,在?ABCD中,对角线AC,BD交于点O,EF是过点O的一条直线,交AB于点E,交DC于点F.则OE与OF有什么数量关系?答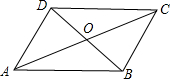 如图,在?ABCD中,∠ADB=90°,OA=6,OB=3,则AD=
如图,在?ABCD中,∠ADB=90°,OA=6,OB=3,则AD= (重点题)在?ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,∠AEF=54°,则∠B=________.
(重点题)在?ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,∠AEF=54°,则∠B=________.