题目内容
 (2013•杭州)射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,
(2013•杭州)射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,| 3 |
t=2或3≤t≤7或t=8
t=2或3≤t≤7或t=8
(单位:秒)分析:求出AB=AC=BC=4cm,MN=
AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,分为三种情况:画出图形,结合图形求出即可;
| 1 |
| 2 |
解答:解:∵△ABC是等边三角形,
∴AB=AC=BC=AM+MB=4cm,∠A=∠C=∠B=60°,
∵QN∥AC,AM=BM.
∴N为BC中点,
∴MN=
AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,
分为三种情况:①如图1,
当⊙P切AB于M′时,连接PM′,
则PM′=
cm,∠PM′M=90°,
∵∠PMM′=∠BMN=60°,
∴M′M=1cm,PM=2MM′=2cm,
∴QP=4cm-2cm=2cm,
即t=2;
②如图2,
当⊙P于AC切于A点时,连接PA,
则∠CAP=∠APM=90°,∠PMA=∠BMN=60°,AP=
cm,
∴PM=1cm,
∴QP=4cm-1cm=3cm,
即t=3,
当⊙P于AC切于C点时,连接P′C,
则∠CP′N=∠ACP′=90°,∠P′NC=∠BNM=60°,CP′=
cm,
∴P′N=1cm,
∴QP=4cm+2cm+1cm=7cm,
即当3≤t≤7时,⊙P和AC边相切;
③如图3,
当⊙P切BC于N′时,连接PN′
则PN′=
cm,∠PN′N=90°,
∵∠PNN′=∠BNM=60°,
∴N′N=1cm,PN=2NN′=2cm,
∴QP=4cm+2cm+2cm=8cm,
即t=8;
故答案为:t=2或3≤t≤7或t=8.
∴AB=AC=BC=AM+MB=4cm,∠A=∠C=∠B=60°,
∵QN∥AC,AM=BM.
∴N为BC中点,
∴MN=
| 1 |
| 2 |
分为三种情况:①如图1,

当⊙P切AB于M′时,连接PM′,
则PM′=
| 3 |
∵∠PMM′=∠BMN=60°,
∴M′M=1cm,PM=2MM′=2cm,
∴QP=4cm-2cm=2cm,
即t=2;
②如图2,

当⊙P于AC切于A点时,连接PA,
则∠CAP=∠APM=90°,∠PMA=∠BMN=60°,AP=
| 3 |
∴PM=1cm,
∴QP=4cm-1cm=3cm,
即t=3,
当⊙P于AC切于C点时,连接P′C,
则∠CP′N=∠ACP′=90°,∠P′NC=∠BNM=60°,CP′=
| 3 |
∴P′N=1cm,
∴QP=4cm+2cm+1cm=7cm,
即当3≤t≤7时,⊙P和AC边相切;
③如图3,

当⊙P切BC于N′时,连接PN′
则PN′=
| 3 |
∵∠PNN′=∠BNM=60°,
∴N′N=1cm,PN=2NN′=2cm,
∴QP=4cm+2cm+2cm=8cm,
即t=8;
故答案为:t=2或3≤t≤7或t=8.
点评:本题考查了等边三角形的性质,平行线的性质,勾股定理,含30度角的直角三角形性质,切线的性质的应用,主要考查学生综合运用定理进行计算的能力,注意要进行分类讨论啊.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目

 (2013•杭州一模)如图是一个由7个同样的立方体叠成的几何体,则这一几何体的三视图中,既是轴对称图形又是中心对称图形的是( )
(2013•杭州一模)如图是一个由7个同样的立方体叠成的几何体,则这一几何体的三视图中,既是轴对称图形又是中心对称图形的是( )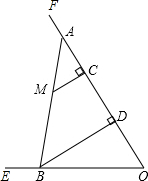 (2013•杭州一模)如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.
(2013•杭州一模)如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.