Question

如图，AB为⊙O的直径，AD为弦，∠DBC=∠A．

（1）求证：BC是⊙O的切线；

（2）连接OC，如果OC恰好经过弦BD的中点E，且tanC=，AD=3，求直径AB的长．

Answer 1

【考点】切线的判定．

【专题】证明题．

【分析】（1）由AB为⊙O的直径，可得∠D=90°，继而可得∠ABD+∠A=90°，又由∠DBC=∠A，即可得∠DBC+∠ABD=90°，则可证得BC是⊙O的切线；

（2）根据点O是AB的中点，点E时BD的中点可知OE是△ABD的中位线，故AD∥OE，则∠A=∠BOC，再由（1）∠D=∠OBC=90°，故∠C=∠ABD，由tanC=可知tan∠ABD=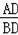=，由此可得出结论．

【解答】（1）证明：∵AB为⊙O的直径，

∴∠D=90°，

∴∠ABD+∠A=90°，

∵∠DBC=∠A，

∴∠DBC+∠ABD=90°，即AB⊥BC，

∴BC是⊙O的切线；

（2）∵点O是AB的中点，点E时BD的中点，

∴OE是△ABD的中位线，

∴AD∥OE，

∴∠A=∠BOC．、

∵由（1）∠D=∠OBC=90°，

∴∠C=∠ABD，

∵tanC=，

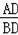
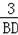
∴tan∠ABD===，解得BD=6，

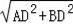
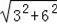
∴AB===3．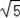

【点评】本题考查的是切线的判定，熟知经过半径的外端且垂直于这条半径的直线是圆的切线是解答此题的关键．