题目内容
正方形ABCD的边长为4,点P是BC边上的动点,点E在AB边上,且∠EPB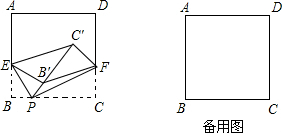 =60°,沿PE翻折△EBP得到△EB′P.F是CD边上一点,沿PF翻折△FCP得到△FC′P,使点C′落在射线PB′上.
=60°,沿PE翻折△EBP得到△EB′P.F是CD边上一点,沿PF翻折△FCP得到△FC′P,使点C′落在射线PB′上.
(1)如图,当BP=1时,四边形EB′FC′的面积为______;
(2)若BP=m,则四边形EB′FC′的面积为______(要求:用含m的代数式表示,并写出m的取值范围).
解:(1)∵BP=1,∠EPB=60°,
∴BE=B'E= ,C'P=CP=BC-BP=3,∠C'PF=∠CPF=30°,
,C'P=CP=BC-BP=3,∠C'PF=∠CPF=30°,
∴C'F=CF=CP×tan∠CPF= ,C'B'=C'P-B'P=3-1=2,
,C'B'=C'P-B'P=3-1=2,
故S四边形EB′FC′=S△EB'C'+S△B'C'F= B'E×B'C'+
B'E×B'C'+ C'F×B'C'=
C'F×B'C'= +
+ =2
=2 ;
;
(2))①∵BP=m,∠EPB=60°,
∴BE=B'E= m,C'P=CP=BC-BP=4-m,∠C'PF=∠CPF=30°,
m,C'P=CP=BC-BP=4-m,∠C'PF=∠CPF=30°,
∴C'F=CF=CP×tan∠CPF= (4-m),C'B'=C'P-B'P=4-m-m=4-2m,
(4-m),C'B'=C'P-B'P=4-m-m=4-2m,
故S四边形EB′FC′=S△EB'C'+S△B'C'F= B'E×B'C'+
B'E×B'C'+ C'F×B'C'
C'F×B'C'
= ×
× m×(4-2m)+
m×(4-2m)+ ×
× (4-m)×(4-2m)
(4-m)×(4-2m)
=- m2+2
m2+2 m+
m+ m2-2
m2-2 m+
m+
=- m2+
m2+ (0<m<2).
(0<m<2).
②当2<m≤ 时,
时,
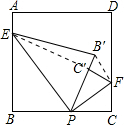
EB'=EB= m,B'C'=m-(4-m)=2m-4,FC'=
m,B'C'=m-(4-m)=2m-4,FC'= (4-m),
(4-m),
故S四边形EB′FC′=S△EB'c'+S△B'C'F= B'E×B'C'+
B'E×B'C'+ C'F×B'C'
C'F×B'C'
= ×
× m×(2m-4)+
m×(2m-4)+ ×(2m-4)×
×(2m-4)× (4-m)
(4-m)
= m2-2
m2-2 m+(m-2)×(
m+(m-2)×( -
- m)
m)
= m2-2
m2-2 m+
m+ m-
m- m2-
m2- +
+ m
m
= m2-
m2- (2<m≤
(2<m≤ ).
).
故答案为:2 ;-
;- m2+
m2+ (0<m<2),
(0<m<2), m2-
m2- (2<m≤
(2<m≤ ).
).
分析:(1)根据BP=1,∠EPB=60°,可得出BE=B'E= ,CP=C'P=4-1=3,也可得出C'F,继而根据S四边形EB′FC′=S△EB'C'+S△B'C'F可得出答案.
,CP=C'P=4-1=3,也可得出C'F,继而根据S四边形EB′FC′=S△EB'C'+S△B'C'F可得出答案.
(2)将BP的长度换为m,按照(1)的思路分别求出各线段的长度,然后求面积即可.
点评:本题考查了正方形的性质及翻折变换的知识,利用解直角三角形的知识求出各线段的长度是解答本题的关键,另外要掌握翻折前后对应边、对应角分别相等.
∴BE=B'E=
 ,C'P=CP=BC-BP=3,∠C'PF=∠CPF=30°,
,C'P=CP=BC-BP=3,∠C'PF=∠CPF=30°,∴C'F=CF=CP×tan∠CPF=
 ,C'B'=C'P-B'P=3-1=2,
,C'B'=C'P-B'P=3-1=2,故S四边形EB′FC′=S△EB'C'+S△B'C'F=
 B'E×B'C'+
B'E×B'C'+ C'F×B'C'=
C'F×B'C'= +
+ =2
=2 ;
;(2))①∵BP=m,∠EPB=60°,
∴BE=B'E=
 m,C'P=CP=BC-BP=4-m,∠C'PF=∠CPF=30°,
m,C'P=CP=BC-BP=4-m,∠C'PF=∠CPF=30°,∴C'F=CF=CP×tan∠CPF=
 (4-m),C'B'=C'P-B'P=4-m-m=4-2m,
(4-m),C'B'=C'P-B'P=4-m-m=4-2m,故S四边形EB′FC′=S△EB'C'+S△B'C'F=
 B'E×B'C'+
B'E×B'C'+ C'F×B'C'
C'F×B'C'=
 ×
× m×(4-2m)+
m×(4-2m)+ ×
× (4-m)×(4-2m)
(4-m)×(4-2m)=-
 m2+2
m2+2 m+
m+ m2-2
m2-2 m+
m+
=-
 m2+
m2+ (0<m<2).
(0<m<2).②当2<m≤
 时,
时,
EB'=EB=
 m,B'C'=m-(4-m)=2m-4,FC'=
m,B'C'=m-(4-m)=2m-4,FC'= (4-m),
(4-m),故S四边形EB′FC′=S△EB'c'+S△B'C'F=
 B'E×B'C'+
B'E×B'C'+ C'F×B'C'
C'F×B'C'=
 ×
× m×(2m-4)+
m×(2m-4)+ ×(2m-4)×
×(2m-4)× (4-m)
(4-m)=
 m2-2
m2-2 m+(m-2)×(
m+(m-2)×( -
- m)
m)=
 m2-2
m2-2 m+
m+ m-
m- m2-
m2- +
+ m
m=
 m2-
m2- (2<m≤
(2<m≤ ).
).故答案为:2
 ;-
;- m2+
m2+ (0<m<2),
(0<m<2), m2-
m2- (2<m≤
(2<m≤ ).
).分析:(1)根据BP=1,∠EPB=60°,可得出BE=B'E=
 ,CP=C'P=4-1=3,也可得出C'F,继而根据S四边形EB′FC′=S△EB'C'+S△B'C'F可得出答案.
,CP=C'P=4-1=3,也可得出C'F,继而根据S四边形EB′FC′=S△EB'C'+S△B'C'F可得出答案.(2)将BP的长度换为m,按照(1)的思路分别求出各线段的长度,然后求面积即可.
点评:本题考查了正方形的性质及翻折变换的知识,利用解直角三角形的知识求出各线段的长度是解答本题的关键,另外要掌握翻折前后对应边、对应角分别相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 附加题
附加题 如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3
如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为 如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=
如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=