题目内容
【题目】已知直线y＝2x＋m与抛物线y＝ax2＋ax＋b有一个公共点M(1，0)，且a＜b.
(1)求抛物线顶点Q的坐标（用含a的代数式表示）；
(2)说明直线与抛物线有两个交点；
(3)直线与抛物线的另一个交点记为N.
①若－1≤a≤一
，求线段MN长度的取值范围；
②求△QMN面积的最小值．
【答案】（1）（-
，-
）（2）证明见解析（3）
【解析】分析: （1）把M点坐标代入抛物线解析式可得到b与a的关系，可用a表示出抛物线解析式，化为顶点式可求得其顶点坐标；
（2）由直线解析式可先求得m的值，联立直线与抛物线解析式，消去y，可得到关于x的一元二次方程，再判断其判别式大于0即可；
（3）①由（2）的方程，可求得N点坐标，利用勾股定理可求得MN2，利用二次函数性质可求得MN长度的取值范围；②设抛物线对称轴交直线与点E，则可求得E点坐标，利用S△QMN=S△QEN+S△QEM可用a表示出△QMN的面积，再整理成关于a的一元二次方程，利用判别式可得其面积的取值范围，可求得答案
详解:
（1）∵M（1，0），
∴b=-2a，
∴y=ax2+ax+b
=ax2+ax-2a
= a(x+)2－
∴顶点Q的坐标为（－，－）.
（2）由直线y=2x+m经过点M（1，0），可得m=－2.
∴y=2x-2
∴ax2+（a-2）x-2a+2=0
∴△=（a-2）2－4×a×（－2a+2）=（3a－2）2
∵2a +b=0，a<b
∴a<0
∴△>0
∴方程有两个不相等的实数根，
∴直线与抛物线有两个交点.
（3）把y=2x-2代入y=ax2+ax-2a，得ax2+（a-2）x-2a+2=0，
即x2+(1-
)x-2+=0，
∴（x-1）（x+2-）=0,
解得x1=1,x2 =-2，
∴点N（-2，
-6）.
（i）根据勾股定理得，
MN2=[（-2）-1]2+（-6）2=20（
）2，
∵-1≤a≤-，
∴-2≤
≤-1，
∴<0，
∴MN=2
（
）=3
，
∴5≤MN≤7.
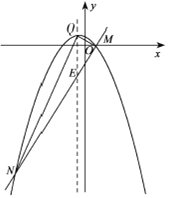
（ii）作直线x=－ 交直线y=2x-2于点E，
把x=－代入y=2x-2得，y=-3，
即E（－，-3），
∵M（1，0），N（-2，-6），且由（2）知a<0，
∴S△QMN =S△QEN+S△QEM= 
=
，
即27a2+(8S-54)a+24=0，
∵关于a的方程有实数根，
∴△=（8S-54）2-4×27×24≥0，
即（8S-54）2≥（36
）2，
又∵a<0，
∴S=>
,
∴8S-54>0，
∴8S-54≥36，即S≥ ，
当S=时，由方程可得a=-
满足题意.
∴△QMN面积的最小值为.
点睛: 本题为二次函数的综合应用，涉及函数图象的交点、二次函数的性质、根的判别式、勾股定理、三角形的面积等知识．在（1）中由M的坐标得到b与a的关系是解题的关键，在（2）中联立两函数解析式，得到关于x的一元二次方程是解题的关键，在（3）中求得N点的坐标是解题的关键，在最后一小题中用a表示出△QMN的面积是解题的关键．本题考查知识点较多，综合性较强，难度较大.
名校课堂系列答案
