题目内容
18.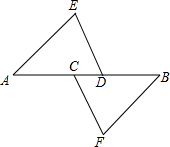 如图:点C、D在AB上,且AC=BD,AE=FB,DE=FC.求证:AE∥BF.
如图:点C、D在AB上,且AC=BD,AE=FB,DE=FC.求证:AE∥BF.
分析 由AC=BD,利用等式的性质得到AD=BC,利用SSS得到三角形AED与三角形FBC全等,利用全等三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.
解答 证明:∵AC=BD,
∴AC+CD=BD+CD,即AD=BC,
在△ADE和△BCF中,
$\left\{\begin{array}{l}{AD=BC}\\{AE=FB}\\{DE=FC}\end{array}\right.$,
∴△ADE≌△BCF(SSS),
∴∠A=∠B,
∴AE∥BF.
点评 此题考查了全等三角形的判定与性质,平行线的判定,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
3.如果等腰三角形有两边长分别是8和4,那么它的周长是( )
| A. | 12 | B. | 16 | C. | 20或16 | D. | 20 |
10.太阳、西瓜、易拉罐、篮球、橡皮擦、书本中,形状类似圆柱的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
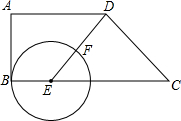 在梯形ABCD中,AD∥BC,AB⊥AD,AB=4,AD=5,CD=5.E为底边BC上一点,以点E为圆心,BE为半径画⊙E交射线ED于点F.设BE=y,DF=x.
在梯形ABCD中,AD∥BC,AB⊥AD,AB=4,AD=5,CD=5.E为底边BC上一点,以点E为圆心,BE为半径画⊙E交射线ED于点F.设BE=y,DF=x.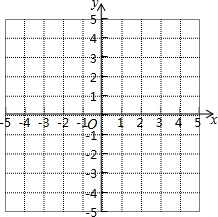 已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{k}{2}$x+m的图象交点为(2,2).
已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{k}{2}$x+m的图象交点为(2,2). 如图,要在一块长方形木板上钻一个孔,孔的中心P到木板右边的距离是15mm,到下边的距离是10mm,请你在图中画出这个孔的中心P所在的位置.如果以AB所在的直线作为x轴(向右为正方向),以BC所在的直线作为y轴(向上为正方向),以1mm为单位长度建立平面直角坐标系,写出孔中心P的坐标.
如图,要在一块长方形木板上钻一个孔,孔的中心P到木板右边的距离是15mm,到下边的距离是10mm,请你在图中画出这个孔的中心P所在的位置.如果以AB所在的直线作为x轴(向右为正方向),以BC所在的直线作为y轴(向上为正方向),以1mm为单位长度建立平面直角坐标系,写出孔中心P的坐标.