题目内容
 如图,已知,DE⊥AC于E,BF⊥AC于F,且AE=CF,DE=BF.
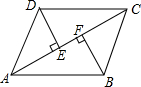
如图,已知,DE⊥AC于E,BF⊥AC于F,且AE=CF,DE=BF.
(1)写出你认为全等的三角形;
(2)求证:∠BAC=∠ACD.
解:(1)△AED≌△CFB,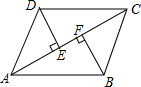 △ABF≌△CDE;
△ABF≌△CDE;
(2)∵AE=CF,
∴AE+EF=CF+FE,
即AF=CE,
∵DE⊥AC于E,BF⊥AC于F,
∴∠AFB=∠CED=90°,
在△ABF和△CDE中,
∵BF=DE,∠AFB=∠CED=90°,AF=CE,
∴△ABF≌△CDE(SAS),
∴∠BAC=∠ACD.
分析:(1)可直接写出△AED≌△CFB,△ABF≌△CDE;
(2)由于DE⊥AC于E,BF⊥AC于F,易知∠AFB=∠CED,而AE=CF,那么AE+EF=CF+EF,即AF=CE,结合DE=BF,利用SAS易证△ABF≌△CDE(SAS),那么可得∠BAC=∠ACD.
点评:本题考查了全等三角形的判定和性质,解题的关键是证明△ABF≌△CDE.
 △ABF≌△CDE;
△ABF≌△CDE;(2)∵AE=CF,
∴AE+EF=CF+FE,
即AF=CE,
∵DE⊥AC于E,BF⊥AC于F,
∴∠AFB=∠CED=90°,
在△ABF和△CDE中,
∵BF=DE,∠AFB=∠CED=90°,AF=CE,
∴△ABF≌△CDE(SAS),
∴∠BAC=∠ACD.
分析:(1)可直接写出△AED≌△CFB,△ABF≌△CDE;
(2)由于DE⊥AC于E,BF⊥AC于F,易知∠AFB=∠CED,而AE=CF,那么AE+EF=CF+EF,即AF=CE,结合DE=BF,利用SAS易证△ABF≌△CDE(SAS),那么可得∠BAC=∠ACD.
点评:本题考查了全等三角形的判定和性质,解题的关键是证明△ABF≌△CDE.

练习册系列答案
相关题目
 如图,已知AB∥DE,AB=DE,AF=DC,求证:四边形BCEF是平行四边形.
如图,已知AB∥DE,AB=DE,AF=DC,求证:四边形BCEF是平行四边形.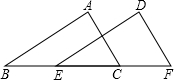 如图,已知AB=DE,AC=DF,要使△ABC≌△DEF,还需要补充一个条件,你补充的条件是:
如图,已知AB=DE,AC=DF,要使△ABC≌△DEF,还需要补充一个条件,你补充的条件是: 如图,已知:DE∥BC,AD:DB=1:2,DE=2,则BC=( )
如图,已知:DE∥BC,AD:DB=1:2,DE=2,则BC=( ) 如图,已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,请补充完整过程,说明△ABC≌△DEF的理由.
如图,已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,请补充完整过程,说明△ABC≌△DEF的理由.
 如图,已知AC∥DE,∠1=∠2.求证:AB∥CD.
如图,已知AC∥DE,∠1=∠2.求证:AB∥CD.