题目内容
已知：定点A（3，2），动点M在函数y=x的图象上运动，动点N在x轴上运动，则△AMN的周长的最小值为分析：作出定点A（3，2），关于函数y=x的对称点A′，A关于x轴的对称点A′′，连接A′A′′，根据线段垂直平分线的性质得到△AMN的周长的最小值为线段A′A′′的长度，求出即可．
解答：解：根据题意画出图形，如图所示：
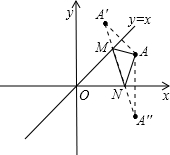
定点A（3，2），关于函数y=x的对称点A′（2，3），
A关于x轴的对称点A′′（3，-2），
A′A′′=
=
．
故答案为：
定点A（3，2），关于函数y=x的对称点A′（2，3），
A关于x轴的对称点A′′（3，-2），
A′A′′=
| (2-3)2+(3+2)2 |
| 26 |
故答案为：
| 26 |
点评：考查了轴对称-最短路线问题
练习册系列答案
快捷英语周周练系列答案
相关题目
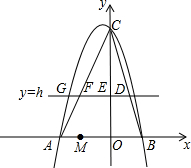（2012•百色）如图，在平面直角坐标系中，抛物线y=ax2+bx+6经过点A（-3，0）和点B（2，0）．直线y=h（h为常数，且0＜h＜6）与BC交于点D，与y轴交于点E，与AC交于点F，与抛物线在第二象限交于点G．
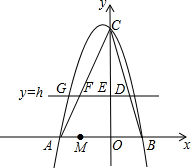如图，在平面直角坐标系中，抛物线y=ax2+bx+6经过点A（-3，0）和点B（2，0）．直线y=h（h为常数，且0＜h＜6）与BC交于点D，与y轴交于点E，与AC交于点F，与抛物线在第二象限交于点G．
