Question

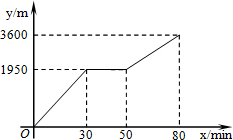（2013•德惠市一模）甲和乙上山游玩，甲乘坐缆车，乙步行，两人相约在山顶的缆车终点会合．已知乙行走到缆车终点的路程是缆车到山顶的线路长的2倍，甲在乙出发后50min才乘上缆车，缆车的平均速度为180m/min．设乙出发xmin后行走的路程为ym．图中的折线表示乙在整个行走过程中y与x的函数关系．
（1）乙行走的总路程是

3600

 m，他途中休息了

20

min．
（2）①当50≤x≤80时，求y与x的函数关系式；
②当甲到达缆车终点时，乙离缆车终点的路程是多少？

Answer 1

分析：（1）通过运用函数图象的分析可以求出乙行走的总路程及途中休息的时间；
（2）直接运用待定系数法就可以求出解析式；
（3）运用乙行驶的全程求出甲行驶的路程，就可以求出甲行驶完全程用的时间，再代入其解析式就可以求出结论．

解答：解：（1）由图象得：
乙行走的总路程是：3600米，他途中休息了20分钟．   
故答案为：3600，20；                 

（2）①当50≤x≤80时，设y与x的函数关系式为y=kx+b．根据题意得：

1950=50k+b 3600=80k+b

，
解得：

k=55 b=-800

，
∴y与x的函数关系式为：y=55x-800        
②缆车到山顶的路线长为3600÷2=1800（m），
缆车到达终点所需时间为1800÷180=10（min）．
甲到达缆车终点时，乙行走的时间为10+50=60（min）．
把x=60代入y=55x-800，得y=55×60-800=2500．
所以，当甲到达缆车终点时，
乙离缆车终点的路程是：3600-2500=1100（m）．

点评：本题是一道有关行程问题的一次函数综合试题，考查了待定系数法求函数的解析式的运用，一次函数图象的性质的运用，在解答时读懂图象是关键．