Question

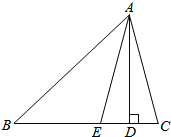
【题目】如图1，点A、D在y轴正半轴上，点B、C分别在x轴上，CD平分∠ACB与y轴交于D点，∠CAO＝90°﹣∠BDO．

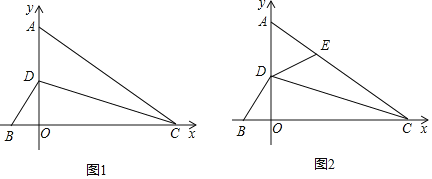
（1）求证：AC＝BC；

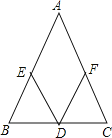
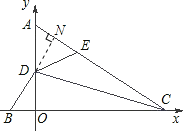
（2）如图2，点C的坐标为（4，0），点E为AC上一点，且∠DEA＝∠DBO，求BC+EC的长．

Answer 1

【答案】（1）见解析；（2）8

【解析】

（1）由题意∠CAO＝90°﹣∠BDO，可知∠CAO＝∠CBD，CD平分∠ACB与y轴交于D点，所以可由AAS定理证明△ACD≌△BCD，由全等三角形的性质可得AC＝BC；

（2）过D作DN⊥AC于N点，可证明Rt△BDO≌Rt△EDN、△DOC≌△DNC，因此，BO＝EN、OC＝NC，所以，BC+EC＝BO+OC+NC﹣NE＝2OC，即可得BC+EC的长．

（1）证明：∵∠CAO＝90°﹣∠BDO，

∴∠CAO＝∠CBD．

在△ACD和△BCD中 ，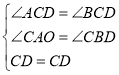

∴△ACD≌△BCD（AAS）．

∴AC＝BC；

（2）由（1）知∠CAD＝∠DEA＝∠DBO，

∴BD＝AD＝DE，过D作DN⊥AC于N点，如图所示：

∵∠ACD＝∠BCD，

∴DO＝DN，

在Rt△BDO和Rt△EDN中 ，

∴Rt△BDO≌Rt△EDN（HL），

∴BO＝EN．

在△DOC和△DNC中，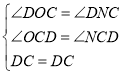

∴△DOC≌△DNC（AAS），

∴OC＝NC；

∴BC+EC＝BO+OC+NC﹣NE＝2OC＝8．