题目内容
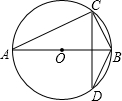如图，已知AB是⊙O的直径，CD是弦，且CD⊥AB，BC=6，AC=8，求sin∠ABD的值．
分析：首先根据垂径定理得出∠ABD=∠ABC，然后由直径所对的圆周角是直角，得出∠ACB=90°，根据勾股定理算出斜边AB的长，再根据正弦的定义求出sin∠ABC的值，从而得出sin∠ABD的值．
解答：解：由条件可知：弧AC=弧AD，则∠ABD=∠ABC，
所以sin∠ABD=sin∠ABC=
；
AB为直径，BC=6，AC=8，可得AB=10，
∴sin∠ABD=
．
所以sin∠ABD=sin∠ABC=
| AC |
| AB |
AB为直径，BC=6，AC=8，可得AB=10，
∴sin∠ABD=
| 4 |
| 5 |
点评：本题主要考查了垂径定理及锐角三角函数的定义．
垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．
在直角三角形中，锐角的正弦为对边比斜边．
垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．
在直角三角形中，锐角的正弦为对边比斜边．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知AB是⊙O的直径，AC是弦，D为AB延长线上一点，DC=AC，∠ACD=120°，BD=10．
如图，已知AB是⊙O的直径，C是⊙O上一点，∠BAC的平分线交⊙O于点D，交⊙O的切线BE于点E，过点D作DF⊥AC，交AC的延长线于点F．
（2013•泰安）如图，已知AB是⊙O的直径，AD切⊙O于点A，点C是
如图，已知AB是⊙O的直径，P为⊙O外一点，且OP∥BC，∠P=∠BAC．
如图，已知AB是圆O的直径，∠DAB的平分线AC交圆O与点C，作CD⊥AD，垂足为点D，直线CD与AB的延长线交于点E．