题目内容
(本小题满分8分) 已知下列n(n为正整数)个关于x的一元二次方程:
①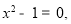 ②
②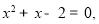 ③
③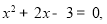
 (n)
(n)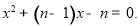
⑴请解上述一元二次方程①、②、③、(n);
⑵请你指出这n 个方程的根具有什么共同特点,写出一条即可。
练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
题目内容
(本小题满分8分) 已知下列n(n为正整数)个关于x的一元二次方程:
①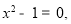 ②
②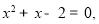 ③
③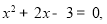
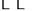 (n)
(n)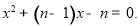
⑴请解上述一元二次方程①、②、③、(n);
⑵请你指出这n 个方程的根具有什么共同特点,写出一条即可。
 出彩同步大试卷系列答案
出彩同步大试卷系列答案