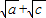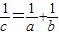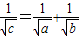题目内容
 如图,已知圆心为C(0,1)的圆与y轴交于A,B两点,与x轴交于D,E两点,且DE=4
如图,已知圆心为C(0,1)的圆与y轴交于A,B两点,与x轴交于D,E两点,且DE=4 .点Q为⊙C上的一个动点,过Q的直线交y轴于点P(0,-8),连结OQ.
.点Q为⊙C上的一个动点,过Q的直线交y轴于点P(0,-8),连结OQ.
(1)直径AB=______;
(2)当点Q与点D重合时,求证:直线PD为圆的切线;
(3)猜想并证明在运动过程中,PQ与OQ之比为一个定值.
 (1)解:∵圆心为C(0,1)的圆与y轴交于A,B两点,与x轴交于D,E两点,且DE=4
(1)解:∵圆心为C(0,1)的圆与y轴交于A,B两点,与x轴交于D,E两点,且DE=4 ,
,∴DO=OE=2
 ,CO=1,
,CO=1,∴CD=3,
∴AB=2×3=6;
(2)证明:连接CD,
∵
 =
= =
= ,
,∠COD=∠DOP=90°,
∴△COD∽△DOP,
∴∠CDO=∠DPO,
∵∠DPO+∠ODP=90°,
∴CD⊥DP,
∵点D在⊙O上,
∴直线PD为圆的切线;
(3)猜想:PQ:OQ=3:1,
证明:作QH⊥y轴于点H,设Q(x,y)
∵点Q在圆上,
∴CQ=3,即QH 2+CH 2=9,
∴x 2+(1-y) 2=9,
分别在Rt△OQH和Rt△PQH中,
得:QO 2=x 2+y2,QP2=x 2+(-8-y)2,
∴QP2=x2-(1-y) 2+(-8-y)2=9(8+2y),
QO 2=x2-(1-y) 2+y2=8+2y,
∴PQ:OQ=3:1.
故答案为:6.
分析:(1)利用垂径定理以及勾股定理求出CD即可得出AB的长;
(2)根据相似三角形的判定和性质得出△COD∽△DOP,进而得出∠CDO=∠DPO,求出CD⊥DP即可得出答案;
(3)利用勾股定理得出:QO 2=x 2+y2,QP2=x 2+(-8-y)2,x 2+(1-y) 2=9,整理得出PQ与OQ的关系.
点评:此题主要考查了圆的综合应用以及相似三角形的判定与性质以及勾股定理等知识,熟练应用相似三角形的判定和性质得出是解题关键.

练习册系列答案
相关题目
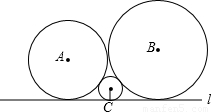
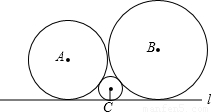
如图,已知圆心为A,B,C的三个圆彼此相切,且均与直线l相切.若⊙A,⊙B,⊙C的半径分别为a,b,c(0<c<a<b),则a,b,c一定满足的关系式为( )
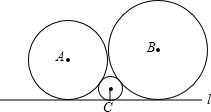

| A、2b=a+c | ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
 (2013•太仓市二模)如图,已知圆心为C(0,1)的圆与y轴交于A,B两点,与x轴交于D,E两点,且DE=4
(2013•太仓市二模)如图,已知圆心为C(0,1)的圆与y轴交于A,B两点,与x轴交于D,E两点,且DE=4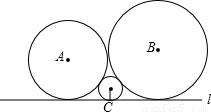
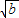 =
=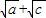
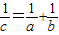
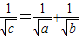
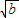 =
=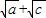
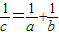
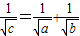
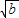 =
=