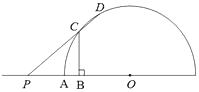
题目内容
【题目】如图,Rt△OAB的顶点A(﹣4,8)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为 
【答案】(2 ![]() ,4)
,4)
【解析】解:∵Rt△OAB的顶点A(﹣4,8)在抛物线y=ax2上,
∴8=16a,解得a= ![]() ,
,
∴抛物线为y= ![]() x2 ,
x2 ,
∵点A(﹣4,8),
∴B(﹣4,0),
∴OB=4,
∵将Rt△OAB绕点O顺时针旋转90°,得到△OCD,
∴D点在y轴上,且OD=OB=4,
∴D(0,4),
∵DC⊥OD,
∴DC∥x轴,
∴P点的纵坐标为4,
代入y= ![]() x2 , 得4=
x2 , 得4= ![]() x2 ,
x2 ,
解得x=±2 ![]() ,
,
∴P(2 ![]() ,4).
,4).
故答案为(2 ![]() ,4).
,4).
先根据待定系数法求得抛物线的解析式,然后根据题意求得D(0,4),且DC∥x轴,从而求得P的纵坐标为4,代入求得的解析式即可求得P的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目