题目内容
 如图,正方形纸张ABCD面积为100cm2,对折一下使D落在BC的D′上,且2D′C=BD′
如图,正方形纸张ABCD面积为100cm2,对折一下使D落在BC的D′上,且2D′C=BD′
(1)求DF的长;
(2)求折痕EF的长.
解:(1)∵正方形纸张ABCD面积为100cm2,
∴CD=CB=10cm,
∵2D′C=BD′,
∴CD′= cm,BD′=
cm,BD′= cm,
cm,
∵正方形纸张ABCD对折使D落在BC的D′上
∴FD′=FD,A′D′=AD=10cm,
设DF=x,则FD′=x,FC=10-x,
在Rt△FCD′中,FC2+CD′2=FD′2,即(10-x)2=( )2+x2,解得x=
)2+x2,解得x=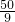 ,
,
∴DF的长为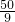 cm;
cm;
(2)∵DF=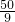 cm,
cm,
∴FC=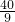 cm,
cm,
设A′D′交AB于G点,如图,
∵∠FD′A′=∠B=90°,
∴∠GD′B+∠FD′C=90°,
而∠FD′C+∠D′FC=90°,
∴∠GD′B=∠D′FC,
∴Rt△GD′B∽Rt△D′FC,
∴ =
= ,即
,即 =
= ,解得GB=5,
,解得GB=5,
∴GD′= =
= ,
,
∴A′G=A′D′-GD′=10- =
= ,
,
∵∠A′GE=∠BGD′,
∴Rt△A′GE∽Rt△BGD′,
∴ =
= ,即
,即 =
= ,解得A′E=
,解得A′E= ,
,
∴AE=DH= ,
,
∴HF=DF-DH= =
= ,
,
过E作EH⊥DC于H,如图,
在Rt△HEF中,EH=AD=10,
EF= =
= (cm).
(cm).
分析:(1)根据正方形的性质得CD=CB=10cm,由2D′C=BD′得到CD′= cm,BD′=
cm,BD′= cm,再根据折叠的性质得FD′=FD,A′D′=AD=10cm,设DF=x,则FD′=x,FC=10-x,利用勾股定理可计算出x=
cm,再根据折叠的性质得FD′=FD,A′D′=AD=10cm,设DF=x,则FD′=x,FC=10-x,利用勾股定理可计算出x=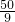 ;
;
(2)设A′D′交AB于G点,过E作EH⊥DC于H,由DF=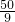 cm得FC=
cm得FC=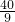 cm,易证Rt△GD′B∽Rt△D′FC,利用相似比可计算出GB=5,根据勾股定理计算出GD′=
cm,易证Rt△GD′B∽Rt△D′FC,利用相似比可计算出GB=5,根据勾股定理计算出GD′= ,则A′G=
,则A′G= ,再证明Rt△A′GE∽Rt△BGD′,利用相似比得A′E=
,再证明Rt△A′GE∽Rt△BGD′,利用相似比得A′E= ,则AE=DH=
,则AE=DH= ,所以HF=DF-DH=
,所以HF=DF-DH= =
= ,在Rt△HEF中,根据勾股定理可计算出EF.
,在Rt△HEF中,根据勾股定理可计算出EF.
点评:本题考查了折叠的性质:折叠前后两图形全等,即对应线段相等,对应角相等;也考查了勾股定理、正方形的性质以及相似三角形的判定与性质.
∴CD=CB=10cm,
∵2D′C=BD′,
∴CD′=
 cm,BD′=
cm,BD′= cm,
cm,∵正方形纸张ABCD对折使D落在BC的D′上
∴FD′=FD,A′D′=AD=10cm,
设DF=x,则FD′=x,FC=10-x,
在Rt△FCD′中,FC2+CD′2=FD′2,即(10-x)2=(
 )2+x2,解得x=
)2+x2,解得x=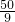 ,
,∴DF的长为
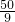 cm;
cm;(2)∵DF=
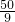 cm,
cm,∴FC=
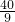 cm,
cm,设A′D′交AB于G点,如图,
∵∠FD′A′=∠B=90°,
∴∠GD′B+∠FD′C=90°,
而∠FD′C+∠D′FC=90°,
∴∠GD′B=∠D′FC,
∴Rt△GD′B∽Rt△D′FC,
∴
 =
= ,即
,即 =
= ,解得GB=5,
,解得GB=5,
∴GD′=
 =
= ,
,∴A′G=A′D′-GD′=10-
 =
= ,
,∵∠A′GE=∠BGD′,
∴Rt△A′GE∽Rt△BGD′,
∴
 =
= ,即
,即 =
= ,解得A′E=
,解得A′E= ,
,∴AE=DH=
 ,
,∴HF=DF-DH=
 =
= ,
,过E作EH⊥DC于H,如图,
在Rt△HEF中,EH=AD=10,
EF=
 =
= (cm).
(cm).分析:(1)根据正方形的性质得CD=CB=10cm,由2D′C=BD′得到CD′=
 cm,BD′=
cm,BD′= cm,再根据折叠的性质得FD′=FD,A′D′=AD=10cm,设DF=x,则FD′=x,FC=10-x,利用勾股定理可计算出x=
cm,再根据折叠的性质得FD′=FD,A′D′=AD=10cm,设DF=x,则FD′=x,FC=10-x,利用勾股定理可计算出x=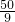 ;
;(2)设A′D′交AB于G点,过E作EH⊥DC于H,由DF=
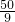 cm得FC=
cm得FC=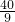 cm,易证Rt△GD′B∽Rt△D′FC,利用相似比可计算出GB=5,根据勾股定理计算出GD′=
cm,易证Rt△GD′B∽Rt△D′FC,利用相似比可计算出GB=5,根据勾股定理计算出GD′= ,则A′G=
,则A′G= ,再证明Rt△A′GE∽Rt△BGD′,利用相似比得A′E=
,再证明Rt△A′GE∽Rt△BGD′,利用相似比得A′E= ,则AE=DH=
,则AE=DH= ,所以HF=DF-DH=
,所以HF=DF-DH= =
= ,在Rt△HEF中,根据勾股定理可计算出EF.
,在Rt△HEF中,根据勾股定理可计算出EF.点评:本题考查了折叠的性质:折叠前后两图形全等,即对应线段相等,对应角相等;也考查了勾股定理、正方形的性质以及相似三角形的判定与性质.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 如图,正方形桌面ABCD,面积为2,铺一块桌布EFGH,点A、B、C、D分别是EF、FG、GH、HE的中点,则桌布EFGH的面积是( )
如图,正方形桌面ABCD,面积为2,铺一块桌布EFGH,点A、B、C、D分别是EF、FG、GH、HE的中点,则桌布EFGH的面积是( ) 17、如图,正方形纸片ABCD,M,N分别是AD,BC的中点,把BC向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,则∠PBQ为( )
17、如图,正方形纸片ABCD,M,N分别是AD,BC的中点,把BC向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,则∠PBQ为( )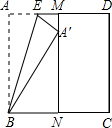 如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M、N分别是AD、BC边的中点,则A′N=
如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M、N分别是AD、BC边的中点,则A′N= 如图,正方形纸张ABCD面积为100cm2,对折一下使D落在BC的D′上,且2D′C=BD′
如图,正方形纸张ABCD面积为100cm2,对折一下使D落在BC的D′上,且2D′C=BD′