题目内容
如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?

【答案】
50.
【解析】
试题分析:过点A作AD⊥BC于D,则垂线段AD的长度为与钓鱼岛A最近的距离,线段CD的长度即为所求.先由方位角的定义得出∠ABC=30°,∠ACD=60°,由三角形外角的性质得出∠BAC=30°,则CA=CB=100海里,然后解直角△ADC,得出CD= AC=50海里.
AC=50海里.
试题解析: 过点A作AD⊥BC于D,

∠ABC=30°,∠ACD=60°,
∴∠BAC=∠ACD-∠ABC=30°,
∴CA=CB.
∵CB=50×2=100(海里),
∴CA=100(海里),
在直角△ADC中,∠ACD=60°,
∴CD= AC=
AC= ×100=50(海里).
×100=50(海里).
故船继续航行50海里与钓鱼岛A的距离最近.
考点: 解直角三角形的应用----方向角问题.

练习册系列答案
相关题目
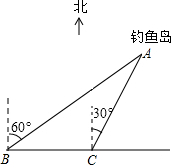 (2013•云南)如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?
(2013•云南)如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?

 如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?
如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?