Question

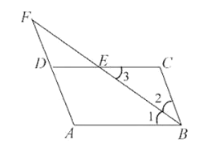
【题目】如图，在菱形中，，，点是线段上一动点，点是线段上一动点，则的最小值（ ）

A.B.C.D.

Answer 1

【答案】D

【解析】

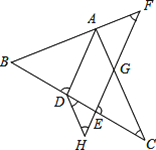
先作点E关于AC的对称点点G，再连接BG，过点B作BH⊥CD于H，运用勾股定理求得BH和GH的长，最后在Rt△BHG中，运用勾股定理求得BG的长，即为PE+PF的最小值．

解：作点E关于AC的对称点点G，连接PG、PE，则PE=PG，CE=CG=2，
连接BG，过点B作BH⊥CD于H，则∠BCH=∠CBH=45°，

∵四边形ABCD是菱形，

∴
∴Rt△BHC中，BH=CH= ，
∴HG=HC-GC=3-2=1，
∴Rt△BHG中，BG= ，
∵当点F与点B重合时，PE+PF=PG+PB=BG（最短），
∴PE+PF的最小值是．
故选：D．