Question

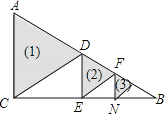
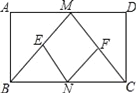
【题目】已知：如图，在矩形ABCD中，，分别是边，的中点，，分别是线段，的中点．

（1）求证：≌；

（2）判断四边形是什么特殊四边形，并证明你的结论；

（3）当四边形是正方形时，求的值．

Answer 1

【答案】（1）证明见解析（2）四边形MENF是菱形（3）2

【解析】分析：(1)因为M为AD中点，根据全等三角形的判定定理推出即可；

(2)根据三角形中位线定理求出NE∥MC，NF=MB，得出平行四边形，求出BM=CM，推出ME=MF，根据菱形的判定推出即可；

(3)求出∠EMF=90°，根据正方形的判定推出即可.

详解：（1）证明：∵四边形是矩形，

∴， 90°，

又∵是的中点， ∴．

在和中，

，

∴≌．

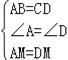（2）解：四边形是菱形．

∵分别是的中点，

∴∥，．

∴四边形是平行四边形．

由（1），得 ∴．

∴四边形是菱形．

（3）解:∵四边形是正方形．

∴，

又∵是的中点，

∴,

∴,

∴,

∴

∴

又∵是的中点，

∴