Question

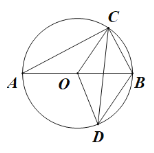
【题目】如图，⊙O的直径AB=10，C、D为⊙O上不同于A、B的两点，OC平分∠ACD，连结BC，BD．

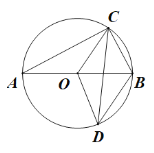
（1）求证：OC∥BD；

（2）过点C作CE⊥DB，垂足为点E．

①求证：△CBE∽△DCE；②若AC=8，求BD的长；

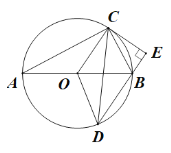
（3）直接写出△BCD面积的最大值．

Answer 1

【答案】（1）见解析；（2）①见解析；②BD=2．8；（3）△BCD面积的最大值为

【解析】

(1)根据同弧所对的圆周角相等得∠BDC=∠BAC，再由半径相等和角平分线定义等量代换得∠OCD=∠CDB即可证明；

(2)①根据(1)的结论和CE⊥DB可得CE⊥OC，进而得∠ECB=∠CDB，即可证明两三角形相似；②根据勾股定理先求BC的长，再证明△ABC和△CBE相似，对应边成比例可求出CE和BE的长，由①中的三角形相似对应边成比例求出DE的长进而求得BD的长；

(3)根据(2)的过程即可表示△BCD的最大面积；

（1）∵∠BDC和∠BAC是同弧所对的圆周角，

∴∠BDC=∠BAC，

∴OA=OC，

∴∠OAC=∠OCA，

∵OC平分∠ACD，

∴∠OCA=∠OCD，

∴∠OCD=∠CDB，

∴OC∥BD；

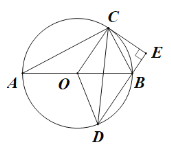
(2)①证明：∵OC∥BD，CE⊥DE，

∴CE⊥OC，

∴∠CEB=90°，

∴∠ECB+∠OCB=90°，

∵AB是直径，

∴∠ACB=90°，

∴∠ACO+∠OCB=90°，

∴∠ACO+∠OCB=90°，

∴∠ECB=∠ACO，

∵∠ACO=∠CDB，

∴∠ECB=∠CDB，∠CEB=∠DEC，

即△CBE△DCE；

②由①得，∠ACO=∠ECB，∠ACB=∠BEC=90°，

∴△ABC△CBE，

∴，

∵Rt△ABC中，AB=10，AC=8，根据勾股定理得，BC=6，

∴，

解得，，

由①得，△CBE△DCE，

∴，

∴，

解得，

∴BD=DE-BE==2.8；

（3）如图：过点O作OG⊥BD于点G，

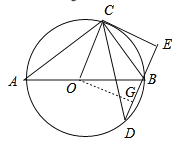
由(2)CE⊥BD，OC⊥CE，

可得四边形COGE是矩形，

∴OC=GE=5，CE=OG，

设BG=x，则BD=2x，BO=5，

在Rt△BGO中，根据勾股定理，得，

，

∴，

即，

∴=，

∴，

∴的最大值为为

∴S的最大值为为；

即△BCD面积的最大值为为；