题目内容
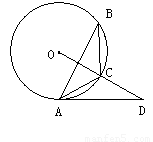
在⊙O中,半径OB垂直于直径MN,过点B的弦BC交MN于点A,分别连接MB,NB,求证:MB•NB=BA•BC.
【答案】分析:先证明△ABN∽△NBC,得 =
= ,即NB•NB=BA•BC,又因为OB⊥MN,得MB=BN,所以MB•NB=BA•BC.
,即NB•NB=BA•BC,又因为OB⊥MN,得MB=BN,所以MB•NB=BA•BC.
解答: 解:连接CN,如图所示:
解:连接CN,如图所示:
由题意得,MB=NB,
∴∠MNB=∠BCN.
∵∠ABN=∠NBC,
∴△ABN∽△NBC.
∴ =
= .
.
即NB•NB=BA•BC,
∵MB=NB,
∴MB•NB=BA•BC.
点评:本题考查了相似三角形的判定与性质.
 =
= ,即NB•NB=BA•BC,又因为OB⊥MN,得MB=BN,所以MB•NB=BA•BC.
,即NB•NB=BA•BC,又因为OB⊥MN,得MB=BN,所以MB•NB=BA•BC.解答:
 解:连接CN,如图所示:
解:连接CN,如图所示:由题意得,MB=NB,
∴∠MNB=∠BCN.
∵∠ABN=∠NBC,
∴△ABN∽△NBC.
∴
 =
= .
.即NB•NB=BA•BC,
∵MB=NB,
∴MB•NB=BA•BC.
点评:本题考查了相似三角形的判定与性质.

练习册系列答案
相关题目
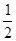 ,∠CAD=30°⑴求证:
,∠CAD=30°⑴求证: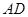 是⊙
是⊙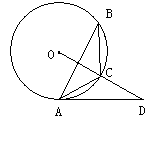
 内接于⊙
内接于⊙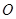 ,点
,点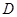 在
在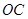 的延长线上,sinB=
的延长线上,sinB=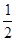 ,∠CAD=30°⑴求证:
,∠CAD=30°⑴求证: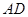 是⊙
是⊙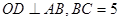 ,求
,求