题目内容
【题目】已知直角三角板![]() 和直角三角板
和直角三角板![]() ,
,![]() ,
,![]() ,
,
![]() .
.
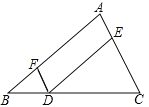
(1)如图1,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 平分
平分![]() 时,求
时,求![]() 的度数;
的度数;
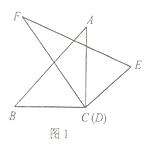
(2)在(1)的条件下,继续旋转三角板![]() ,猜想
,猜想![]() 与
与![]() 有怎样的数量关系?并利用图2所给的情形说明理由;
有怎样的数量关系?并利用图2所给的情形说明理由;
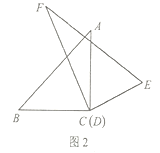
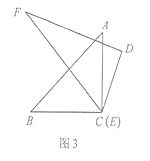
(3)如图3,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 落在
落在![]() 内部时,直接写出
内部时,直接写出![]() 与
与![]() 的数量关系.
的数量关系.
【答案】(1)![]() ;(2)
;(2)![]() , 理由见解析;(3)
, 理由见解析;(3)![]() .
.
【解析】
(1)利用角平分线的定义求出∠ACF=45°,然后利用余角的性质求解即可;
(2)依据同角的余角相等即可求解;
(3)∠ACD与∠BCF都与∠ACF关系紧密,分别表示它们与∠ACF的关系即可求解.
(1)∵CF是∠ACB的平分线,∠ACB=90°,
∴∠ACF=90°÷2=45°,
又∵∠FCE=90°,
∴∠ACE=∠FCE﹣∠ACF=90°﹣45°=45°;
(2)∵∠BCF+∠ACF=90°,
∠ACE+∠ACF=90°,
∴∠BCF=∠ACE;
(3)∵∠FCA=∠FCD﹣∠ACD=60°﹣∠ACD,
∠FCA=∠ACB﹣∠BCF=90°﹣∠BCF,
∴60°﹣∠ACD=90°﹣∠BCF,
∠ACD=30°﹣∠BCF.

 快捷英语周周练系列答案
快捷英语周周练系列答案【题目】如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD对折,使它落在斜边AB上,且与AE重合,则CD等于( )
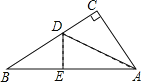
A. 3cmB. 4cmC. 5cmD. 6cm
【题目】先填写表,通过观察后再回答问题:
a | …… | 0.0001 | 0.01 | 1 | 100 | 10000 | …… |
| …… | 0.01 | x | 1 | y | 100 | …… |
(1)表格中,x=_________,y=_________
(2)从表格中探究a与![]() 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知![]() ,则
,则![]() ≈___________
≈___________
②已知![]() ,若
,若![]() ,用含m的代数式表示b,则b=___________
,用含m的代数式表示b,则b=___________
(3)试比较![]() 与a的大小(直接写出结果)
与a的大小(直接写出结果)