Question

如图1，在等腰梯形ABCD中，AB∥DC，AD＝BC＝4 cm，AB＝12 cm，CD＝8 cm点P从A开始沿AB边向B以3 cm/s的速度移动，点Q从C开始沿CD边向D以1 cm/s的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达终点时，另一点也随之停止运动．设运动时间为t(s)．

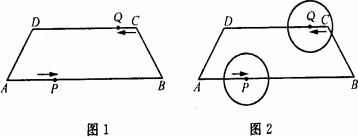
(1)t为何值时，四边形APQD是平等四边形？

(2)如图2，如果⊙P和⊙Q的半径都是2 cm，那么，t为何值时，⊙P和⊙P外切？

Answer 1

答案：
解析：

解：(1)∵DQ∥AP，∴当AP＝DQ时，四边形APQD是平行四边形．此时，3t＝8－t．解得t＝2(s)．即当t为2 s时，四边形APQD是平行四边形． 　　(2)∵⊙P和⊙Q的半径都是2 cm，∴当PQ＝4 cm时，⊙P和⊙Q外切．而当PQ＝4 cm时，如果PQ∥AD，那么四边形APQD是平行四边形． 　　①当四边形APQD是平行四边形时，由(1)得t＝2(s)． 　　②当四边形APQD是等腰梯形时，∠A＝∠APQ．∵在等腰梯形ABCD中，∠A＝∠B，∴∠APQ＝∠B．∴PQ∥BC．∴四边形PBCQ平行四边形．此时，CQ＝PB．∴t＝12－3t．解得t3(s)． 　　综上，当t为2 s或3 s时，⊙P和⊙Q相切．