题目内容
【题目】在平面直角坐标系xOy中，若点P的横坐标和纵坐标相等，则称点P为完美点．已知二次函数
的图象上有且只有一个完美点
，且当
时，函数
的最小值为﹣3，最大值为1，则m的取值范围是（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
根据完美点的概念令ax2+4x+c=x，即ax2+3x+c=0，由题意方程有两个相等的实数根，求得4ac=9，再根据方程的根为
=
，从而求得a=-1，c=-
，所以函数y=ax2+4x+c-
=-x2+4x-3，根据函数解析式求得顶点坐标与纵坐标的交点坐标，根据y的取值，即可确定x的取值范围．
解：令ax2+4x+c=x，即ax2+3x+c=0，
由题意，△=32-4ac=0，即4ac=9，
又方程的根为=，
解得a=-1，c=-，
故函数y=ax2+4x+c-=-x2+4x-3，
如图，该函数图象顶点为（2，1），与y轴交点为（0，-3），由对称性，该函数图象也经过点（4，-3）．
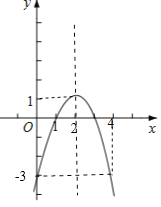
由于函数图象在对称轴x=2左侧y随x的增大而增大，在对称轴右侧y随x的增大而减小，且当0≤x≤m时，函数y=-x2+4x-3的最小值为-3，最大值为1，
∴2≤m≤4，
故选：C．
练习册系列答案
相关题目
