题目内容
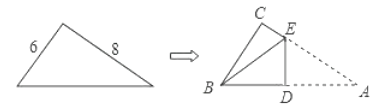
【题目】如图，直角三角形纸片的两直角边长分别为6.8，按如图那样折叠，使点A与点B重合，折痕为DE，求△BDE的面积.
【答案】
【解析】
设CE=
，则AE=AC-CE=8-由折叠点A与点B重合可知BE=AE=8- ， 利用勾股定理可得在直角三角形BCE中，BC2+CE2=BE2可得方程62+2=（8-）2 解得 
可得S△BCE=
可得S△ABE=S△ABC-S△BCE=
即可知： 
解：设CE=，则AE=AC-CE=8-
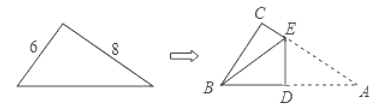
∵折叠点A与点B重合
∴BE=AE=8-
在直角三角形BCE中，
∵BC2+CE2=BE2
∴62+2=（8-）2
解得
∴S△BCE=
∴S△ABE=S△ABC-S△BCE=
由折叠性质可知S△BDE=
S△ABE=
练习册系列答案
相关题目
