题目内容
已知0<x<1,那么在x,| 1 |
| x |
| x |
分析:根据0<x<1,利用不等式的基本性质分别求出x,
,
,x2的取值范围,再根据各数的取值范围即可判断出最大的数.
| 1 |
| x |
| x |
解答:解:∵0<x<1,∴
>1,
∴0<x2<x,
∴0<x<
,
∴
>
>x>x2,
故最大的数是
.
| 1 |
| x |
∴0<x2<x,
∴0<x<
| x |
∴
| 1 |
| x |
| x |
故最大的数是
| 1 |
| x |
点评:本题考查的是实数的大小比较及不等式的基本性质,能根据不等式的基本性质判断出各数的取值范围是解答此题的关键.

练习册系列答案
相关题目
 如图,在菱形ABCD中,已知AB=10,AC=16,那么菱形ABCD的面积为
如图,在菱形ABCD中,已知AB=10,AC=16,那么菱形ABCD的面积为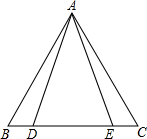 已知AB=AC,AD=AE,那么BD=CE,请说明理由.
已知AB=AC,AD=AE,那么BD=CE,请说明理由.