题目内容
 如图,AB为⊙O的直径,C为⊙O上一动点,过C作B点处切线的垂线,垂足为D,则下列结论中正确的有________.
如图,AB为⊙O的直径,C为⊙O上一动点,过C作B点处切线的垂线,垂足为D,则下列结论中正确的有________.
①BC2=AB•CD;②sin∠ABC=cos∠BCD;③tan∠ABC=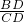 ;④AC>BD;⑤
;④AC>BD;⑤ .
.
①③④⑤
分析:由BD为圆O的切线,得到AB与BD垂直,得到一对角互余,再由CD垂直于BD得到直角三角形BCD中两锐角互余,利用同角的余角相等得到∠ABC=∠BCD,进而得到sin∠ABC=sin∠BCD≠cos∠BCD,选项②错误;利用两对对应角相等的两三角形相似得到三角形ABC与三角形CBD相似,由相似得比例,变形后得到①与⑤正确;在直角三角形BCD中,利用锐角三角函数定义表示出tan∠BCD,即为tan∠ABC,得到选项③正确;C在运动过程中,由斜边大于直角边得到AC大于BD,故选项④正确.
解答:∵BD为圆O的切线,
∴∠ABD=90°,即∠ABC+∠CBD=90°,
∵CD⊥BD,∴∠CBD+∠BCD=90°,
∴∠ABC=∠BCD,
∴△ABC∽△CBD,
∴ =
=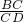 =
= ,即BC2=AB•CD,故选项①正确;
,即BC2=AB•CD,故选项①正确;
∴sin∠ABC=sin∠BCD≠cos∠BCD,选项②错误;
由tan∠ABC=tan∠BCD=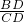 ,选项③正确;
,选项③正确;
而无论C如何移动均有AC>BC,选项④正确;
由相似关系得 =
=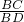 ,故选项⑤正确.
,故选项⑤正确.
故答案为:①③④⑤
点评:此题考查了切线的性质,相似三角形的判定与性质,以及锐角三角函数定义,熟练掌握切线的性质是解本题的关键.
分析:由BD为圆O的切线,得到AB与BD垂直,得到一对角互余,再由CD垂直于BD得到直角三角形BCD中两锐角互余,利用同角的余角相等得到∠ABC=∠BCD,进而得到sin∠ABC=sin∠BCD≠cos∠BCD,选项②错误;利用两对对应角相等的两三角形相似得到三角形ABC与三角形CBD相似,由相似得比例,变形后得到①与⑤正确;在直角三角形BCD中,利用锐角三角函数定义表示出tan∠BCD,即为tan∠ABC,得到选项③正确;C在运动过程中,由斜边大于直角边得到AC大于BD,故选项④正确.
解答:∵BD为圆O的切线,
∴∠ABD=90°,即∠ABC+∠CBD=90°,
∵CD⊥BD,∴∠CBD+∠BCD=90°,
∴∠ABC=∠BCD,
∴△ABC∽△CBD,
∴
 =
=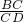 =
= ,即BC2=AB•CD,故选项①正确;
,即BC2=AB•CD,故选项①正确;∴sin∠ABC=sin∠BCD≠cos∠BCD,选项②错误;
由tan∠ABC=tan∠BCD=
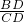 ,选项③正确;
,选项③正确;而无论C如何移动均有AC>BC,选项④正确;
由相似关系得
 =
=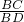 ,故选项⑤正确.
,故选项⑤正确.故答案为:①③④⑤
点评:此题考查了切线的性质,相似三角形的判定与性质,以及锐角三角函数定义,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )| A、1cm | B、2cm | C、3cm | D、4cm |
 如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为