Question

如图，点A，B，C，D是直径为AB的⊙O上四个点，C是劣弧

BD

的中点，AC交BD于点E，AE=2，EC=1．
（1）求证：△DEC∽△ADC；
（2）试探究四边形ABCD是否是梯形？若是，请你给予证明并求出它的面积；若不是，请说明理由．
（3）延长AB到H，使BH=OB．求证：CH是⊙O的切线．

Answer 1

分析：（1）C是劣弧

BD

的中点，根据等弧所对的圆周角相等就可以证明角相等，从而证明△DEC∽△ADC；
（2）首先利用（1）的结论求出DC，再利用勾股定理计算AB，根据计算结果可以判定四边形OBCD是菱形，然后判断四边形ABCD是梯形；
（3）利用（2）的结论OC⊥BD，OG=GC，再利用平行线的判定方法知道BG∥CH，这样根据切线的判定方法就可以判定了．

解答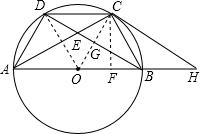：（1）证明：∵C是劣弧

BD

的中点，
∴∠DAC=∠CDB．（1分）
∵∠ACD=∠ACD，
∴△DEC∽△ADC．（3分）

（2）解：连接OD，
∵

DC

AC

=

EC

DC

，
∵CE=1，AC=AE+EC=2+1=3，
∴DC²=AC•EC=3×1=3．
∴DC=

3

．（4分）
∴BC=DC=

3

，
∵AB是⊙O的直径，
∴∠ACB=90°．
∴AB²=AC²+CB²=3²+（

3

）²=12．
∴AB=2

3

．
∴OD=OB=BC=DC=

3

．
∴四边形OBCD是菱形．
∴DC∥AB，DC＜AB．
∴四边形ABCD是梯形．（5分）
法一：
过C作CF垂直AB于F，连接OC，则OB=BC=OC=

3

，
∴∠OBC=60°．（6分）
∴sin60°=

CF

BC

，
CF=BC•sin60°=

3

×

3

2

=

3

2

．
∴S_梯形ABCD=

1

2

CF（AB+DC）=

1

2

×

3

2

(2

3

+

3

)=

9 3

4

．（7分）
法二：（接上证得四边形ABCD是梯形）
∵DC∥AB，
∴AD=BC．
连接OC，则△AOD，△DOC和△OBC的边长均为

3

的等边三角形．（6分）
∴△AOD≌△DOC≌△OBC．
∴S_梯形ABCD=3•S_△AOD=3×

3

4

×(

3

)2=

9 3

4

．（7分）

（3）证明：连接OC交BD于G．
由（2）得四边形OBCD是菱形．
∴OC⊥BD且OG=GC．（8分）
∵OB=BH，
∴BG∥CH．（9分）
∴∠OCH=∠OGB=90°．
∴CH是⊙O的切线．（10分）

点评：此题综合性比较强，把梯形放在圆中，解题利用了梯形的判定和面积公式，解直角三角形，圆的切线的判定等几个知识点．