题目内容
若m、n满足m2+3m-2=0,n2+3n-2=0,求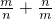 的值.
的值.
解:∵m2+3m-2=0,n2+3n-2=0,
∴当m=n时,原式=1+1=2;
当m≠n时,m、n可看作一元二次方程x2+3x-2=0的两不等根,
∴m+n=-3,mn=-2,
∴原式= =
= =
= =-
=- ,
,
∴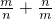 的值为2或-
的值为2或- .
.
分析:由于m2+3m-2=0,n2+3n-2=0,则当m=n时,易得原式=2;当m≠n时,可以把m、n看作一元二次方程x2+3x-2=0的两不等根,根据根与系数的关系得到m+n=-3,mn=-2,再把原式变形得到原式= =
= ,然后利用整体代入的思想计算即可.
,然后利用整体代入的思想计算即可.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=- ,x1•x2=
,x1•x2= .
.
∴当m=n时,原式=1+1=2;
当m≠n时,m、n可看作一元二次方程x2+3x-2=0的两不等根,
∴m+n=-3,mn=-2,
∴原式=
 =
= =
= =-
=- ,
,∴
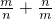 的值为2或-
的值为2或- .
.分析:由于m2+3m-2=0,n2+3n-2=0,则当m=n时,易得原式=2;当m≠n时,可以把m、n看作一元二次方程x2+3x-2=0的两不等根,根据根与系数的关系得到m+n=-3,mn=-2,再把原式变形得到原式=
 =
= ,然后利用整体代入的思想计算即可.
,然后利用整体代入的思想计算即可.点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-
 ,x1•x2=
,x1•x2= .
. 
练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目