��Ŀ����
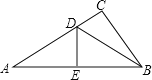
��ͼ����֪��ABCD�У�AD=3cm��CD=1cm����B=45�㣬��P�ӵ�A��������AD���������˶����ٶ�Ϊ3cm/s����Q�ӵ�C��������CD���������˶����ٶ�Ϊ1cm/s�����Ӳ��ӳ�QP��BA���ӳ����ڵ�M����M��MN��BC��������N�����˶�ʱ��Ϊt��s����0��t��1��������������⣺
��1���Ƿ����ʱ��t��ʹ��P�ڡ�BCD��ƽ�����ϣ�
��2�����ı���ANPM�����ΪS��cm²������S��t֮��ĺ�����ϵʽ��
��3���Ƿ����ijһʱ��t��ʹ�ı���ANPM���ABCD�����ȣ������ڣ������Ӧ��tֵ���������ڣ�˵�����ɣ�
��4����tΪ��ֵʱ����ABNΪ���������Σ�


����ͼ
��ϰ��ϵ�д�
�����Ŀ


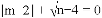 ����m��nǡ���ǵ�����ABC�������ߵı߳������ABC���ܳ��� �� ��
����m��nǡ���ǵ�����ABC�������ߵı߳������ABC���ܳ��� �� ��
 ��tan37���
��tan37��� ��
�� ��1.73��
��1.73��
 ����
���� �ɻ���Ϊ_____________��
�ɻ���Ϊ_____________��
 ��
��