题目内容
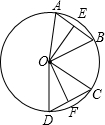如图，在⊙O中，OE⊥AB于点E，OF⊥CD于点F，要使OE=OF，则需添加条件是________（只要写出一种情形即可）．
AB=CD
分析：由△OAB和△OCD是等腰三角形，根据等腰三角形三线合一的性质可得AE=CF，从而可以证明△OAE≌△OCF，则OE=OF．
解答：∵OA=OB，∴△OAB和△OCD是等腰三角形，
∵OE⊥AB，OF⊥CD，∴AE=CF，
∴△OAE≌△OCF，∴OE=OF，
故答案为AB=CD．
点评：本题是一道开放性的题目，考查了垂径定理和勾股定理，以及三角形的全等，要熟练掌握．
分析：由△OAB和△OCD是等腰三角形，根据等腰三角形三线合一的性质可得AE=CF，从而可以证明△OAE≌△OCF，则OE=OF．
解答：∵OA=OB，∴△OAB和△OCD是等腰三角形，
∵OE⊥AB，OF⊥CD，∴AE=CF，
∴△OAE≌△OCF，∴OE=OF，
故答案为AB=CD．
点评：本题是一道开放性的题目，考查了垂径定理和勾股定理，以及三角形的全等，要熟练掌握．
练习册系列答案
名校课堂系列答案
相关题目
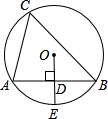如图，在⊙O中，OE为半径，点D为OE的中点，AB是过点D且垂直于OE的弦，点C是优弧ACB上任意一点，则∠ACB度数是（ ）| A、30° | B、50° | C、60° | D、无法确定 |
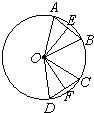16、如图，在⊙O中，OE⊥AB于点E，OF⊥CD于点F，要使OE=OF，则需添加条件是
