题目内容
数学拓展课上，老师定义了一种运算“*”，对于n∈N*，满足以下运算性质：（1）.2*2=1，（2）．（2n+2）*2=3（2n*2），则2n*2用含n的代数式表示为______．
解：∵2※2=1，（2n+2）※2=3（2n※2），
∴[2（n+1）※2]÷（2n※2）=3
∴{ （2n※2）}是以1为首项，3为公比的等比数列，
∴第n项是：3n-1．
故答案是：为 3n-1．
分析：根据：①2※2=1；②（2n+2）※2=3（2n※2），判断数列{（2n※2）}是等比数列，即可求得其通项公式．
点评：本题考查对新定义的理解及等比数列的定义和通项公式的求法，旨在考查学生的观察分析和归纳能力，属基础题．
∴[2（n+1）※2]÷（2n※2）=3
∴{ （2n※2）}是以1为首项，3为公比的等比数列，
∴第n项是：3n-1．
故答案是：为 3n-1．
分析：根据：①2※2=1；②（2n+2）※2=3（2n※2），判断数列{（2n※2）}是等比数列，即可求得其通项公式．
点评：本题考查对新定义的理解及等比数列的定义和通项公式的求法，旨在考查学生的观察分析和归纳能力，属基础题．
练习册系列答案
相关题目
6、某节英语课上，老师布置了10道选择题作为达标练习，小明将全班同学的解题情况绘成图所示的统计图，根据图表，请问中位数是（ ）
；小华：
；小军：
；小强：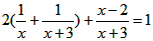
，老师看了同学们的答案，表扬了同学们积极动脑，并给出了如下结论：其中三位同学的结论正确，有一位同学的结论是错误的，你能知道这是为什么吗？