题目内容
 如图所示:OABC是正方形,OD∥AC.|AD|=|AC|,若|OA|=1,则D的坐标是
如图所示:OABC是正方形,OD∥AC.|AD|=|AC|,若|OA|=1,则D的坐标是
- A.(
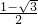 ,
, )
) - B.(
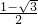 ,
, )
) - C.(
 ,
, )
) - D.(
 ,
, )
)
B
分析:过D作DE垂直于x轴,连接AC,由四边形ABCO为正方形,根据正方形的对角线平分一组对角,且四个内角都为直角,得到∠CAO=45°,由OD与AC平行,根据两直线平行,同位角相等可得∠DOE=45°,进而得到三角形ODE为等腰直角三角形,同时由正方形的边长为1,求出对角线|AC|的长,可设|DE|=|OE|=x,根据|OE|+|OA|表示出|AE|,在直角三角形ADE中,根据勾股定理列出关于x的方程,求出方程的解即可得到x的值,再由D为第二象限的点,确定出D的坐标.
解答: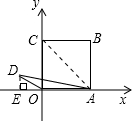 解:过D作x轴的垂线,垂足为E,
解:过D作x轴的垂线,垂足为E,
∵四边形ABCO为正方形,AC为对角线,|OA|=1,
∴∠CAO=45°,|AC|= ,
,
又OD∥AC,
∴∠DOE=45°,
∴△DOE为等腰直角三角形,且|AC|=|AD|= ,
,
设|DE|=|OE|=x,|AE|=x+1,
在Rt△ADE中,根据勾股定理得:|DE|2+|AE|2=|AD|2,
即x2+(x+1)2=( )2,
)2,
整理得:2x2+2x-1=0,
解得:x1=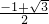 ,x2=
,x2=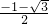 (舍去),
(舍去),
∴|DE|=|OE|= ,
,
则D的坐标为(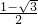 ,
, ).
).
故选B
点评:此题考查了正方形的性质,等腰直角三角形的性质,平行线的性质,平面直角坐标系与坐标以及勾股定理的应用,作出辅助线DE,构造直角三角形,利用勾股定理求出|DE|及|OE|的长是确定D坐标的关键.
分析:过D作DE垂直于x轴,连接AC,由四边形ABCO为正方形,根据正方形的对角线平分一组对角,且四个内角都为直角,得到∠CAO=45°,由OD与AC平行,根据两直线平行,同位角相等可得∠DOE=45°,进而得到三角形ODE为等腰直角三角形,同时由正方形的边长为1,求出对角线|AC|的长,可设|DE|=|OE|=x,根据|OE|+|OA|表示出|AE|,在直角三角形ADE中,根据勾股定理列出关于x的方程,求出方程的解即可得到x的值,再由D为第二象限的点,确定出D的坐标.
解答:
 解:过D作x轴的垂线,垂足为E,
解:过D作x轴的垂线,垂足为E,∵四边形ABCO为正方形,AC为对角线,|OA|=1,
∴∠CAO=45°,|AC|=
 ,
,又OD∥AC,
∴∠DOE=45°,
∴△DOE为等腰直角三角形,且|AC|=|AD|=
 ,
,设|DE|=|OE|=x,|AE|=x+1,
在Rt△ADE中,根据勾股定理得:|DE|2+|AE|2=|AD|2,
即x2+(x+1)2=(
 )2,
)2,整理得:2x2+2x-1=0,
解得:x1=
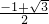 ,x2=
,x2=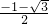 (舍去),
(舍去),∴|DE|=|OE|=
 ,
,则D的坐标为(
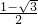 ,
, ).
).故选B
点评:此题考查了正方形的性质,等腰直角三角形的性质,平行线的性质,平面直角坐标系与坐标以及勾股定理的应用,作出辅助线DE,构造直角三角形,利用勾股定理求出|DE|及|OE|的长是确定D坐标的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
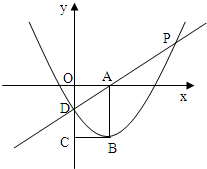 如图所示:A是x轴正半轴上的一个动点,以OA为边在x轴下方作矩形OABC,使
如图所示:A是x轴正半轴上的一个动点,以OA为边在x轴下方作矩形OABC,使 (2013•甘井子区二模)矩形OABC在平面直角坐标系中的位置如图所示,O为坐标原点,OA与y轴重合,OC与x轴重合,M为BC上点,沿AM折叠矩形使得点B′落在OC上,且知OA=6,OB′=8,则点M坐标是
(2013•甘井子区二模)矩形OABC在平面直角坐标系中的位置如图所示,O为坐标原点,OA与y轴重合,OC与x轴重合,M为BC上点,沿AM折叠矩形使得点B′落在OC上,且知OA=6,OB′=8,则点M坐标是
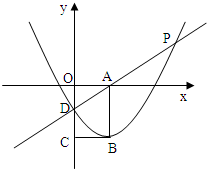 如图所示:A是x轴正半轴上的一个动点,以OA为边在x轴下方作矩形OABC,使
如图所示:A是x轴正半轴上的一个动点,以OA为边在x轴下方作矩形OABC,使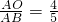 ,将点B沿经过A点的某直线对折到OC边上D点处,以B为顶点的抛物线y=ax2+bx+c (a≠0)经过D点,并且与过A、D两点的直线y=mx+n交于P点.
,将点B沿经过A点的某直线对折到OC边上D点处,以B为顶点的抛物线y=ax2+bx+c (a≠0)经过D点,并且与过A、D两点的直线y=mx+n交于P点.