ΧβΡΩΡΎ»ί
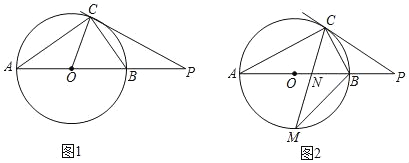
ΓΨΧβΡΩΓΩ‘ΎRtΓςABC÷–Θ§ΓœACB=90ΓψΘ§AB=![]() Θ§AC=2Θ§ΙΐΒψBΉς÷±œΏmΓΈACΘ§ΫΪΓςABC»ΤΒψCΥ≥ ±’κ–ΐΉΣΒΟΒΫΓςAΓδBΓδC(ΒψAΘ§BΒΡΕ‘”ΠΒψΖ÷±πΈΣA'Θ§BΓδ)Θ§…δœΏCAΓδΘ§CBΓδΖ÷³eΫΜ÷±œΏm”ΎΒψPΘ§QΘ°
Θ§AC=2Θ§ΙΐΒψBΉς÷±œΏmΓΈACΘ§ΫΪΓςABC»ΤΒψCΥ≥ ±’κ–ΐΉΣΒΟΒΫΓςAΓδBΓδC(ΒψAΘ§BΒΡΕ‘”ΠΒψΖ÷±πΈΣA'Θ§BΓδ)Θ§…δœΏCAΓδΘ§CBΓδΖ÷³eΫΜ÷±œΏm”ΎΒψPΘ§QΘ°
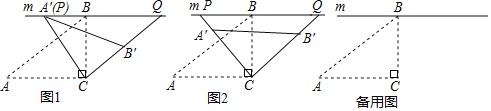
(1)»γΆΦ1Θ§Β±P”κAΓδ÷ΊΚœ ±Θ§«σΓœACAΓδΒΡΕ» ΐΘΜ
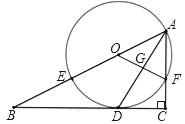
(2)»γΆΦ2Θ§…ηAΓδBΓδ”κBCΒΡΫΜΒψΈΣMΘ§Β±MΈΣAΓδBΓδΒΡ÷–Βψ ±Θ§«σœΏΕΈPQΒΡ≥ΛΘΜ
(3)‘Ύ–ΐΉΣΙΐ≥Χ÷–Θ§Β±ΒψPΘ§QΖ÷±π‘ΎCAΓδΘ§CBΓδΒΡ―”≥ΛœΏ…œ ±Θ§ ‘ΧΫΨΩΥΡ±Ώ–ΈPA'BΓδQΒΡΟφΜΐ «Ζώ¥φ‘ΎΉν–Γ÷ΒΘ°»τ¥φ‘ΎΘ§«σ≥ωΥΡ±Ώ–ΈPAΓδBΓδQΒΡΉν–ΓΟφΜΐΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©60ΓψΘΜΘ®2Θ©PQΘΫ![]() ΘΜΘ®3Θ©¥φ‘ΎΘ§SΥΡ±Ώ–ΈPA'BΓδQΘΫ3©¹
ΘΜΘ®3Θ©¥φ‘ΎΘ§SΥΡ±Ώ–ΈPA'BΓδQΘΫ3©¹![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©”…–ΐΉΣΩ…ΒΟΘΚAC=A'C=2Θ§ΫχΕχΒΟΒΫBC![]() Θ§“άΨίΓœA'BC=90ΓψΘ§Ω…ΒΟcosΓœA'CB
Θ§“άΨίΓœA'BC=90ΓψΘ§Ω…ΒΟcosΓœA'CB![]() Θ§Φ¥Ω…ΒΟΒΫΓœA'CB=30ΓψΘ§ΓœACA'=60ΓψΘΜ
Θ§Φ¥Ω…ΒΟΒΫΓœA'CB=30ΓψΘ§ΓœACA'=60ΓψΘΜ
Θ®2Θ©ΗυΨίMΈΣA'B'ΒΡ÷–ΒψΘ§Φ¥Ω…ΒΟ≥ωΓœA=ΓœA'CMΘ§ΫχΕχΒΟΒΫPB![]() BC
BC![]() Θ§“άΨίtanΓœQ=tanΓœA
Θ§“άΨίtanΓœQ=tanΓœA![]() Θ§Φ¥Ω…ΒΟΒΫBQ=BC
Θ§Φ¥Ω…ΒΟΒΫBQ=BC![]() 2Θ§ΫχΕχΒΟ≥ωPQ=PB+BQ
2Θ§ΫχΕχΒΟ≥ωPQ=PB+BQ![]() ΘΜ
ΘΜ
Θ®3Θ©“άΨίSΥΡ±Ώ–ΈPA'B'Q=SΓςPCQ©¹SΓςA'CB'=SΓςPCQ![]() Θ§Φ¥Ω…ΒΟΒΫSΥΡ±Ώ–ΈPA'B'QΉν–ΓΘ§Φ¥SΓςPCQΉν–ΓΘ§ΕχSΓςPCQ
Θ§Φ¥Ω…ΒΟΒΫSΥΡ±Ώ–ΈPA'B'QΉν–ΓΘ§Φ¥SΓςPCQΉν–ΓΘ§ΕχSΓςPCQ![]() PQΓΝBC
PQΓΝBC![]() PQΘ§άϊ”ΟΦΗΚΈΖ®Φ¥Ω…ΒΟΒΫSΓςPCQΒΡΉν–Γ÷Β=3Θ§Φ¥Ω…ΒΟΒΫΫα¬έΘ°
PQΘ§άϊ”ΟΦΗΚΈΖ®Φ¥Ω…ΒΟΒΫSΓςPCQΒΡΉν–Γ÷Β=3Θ§Φ¥Ω…ΒΟΒΫΫα¬έΘ°
Θ®1Θ©”…–ΐΉΣΩ…ΒΟΘΚAC=A'C=2Θ°
ΓΏΓœACB=90ΓψΘ§AB![]() Θ§AC=2Θ§ΓύBC
Θ§AC=2Θ§ΓύBC![]() Θ°
Θ°
ΓΏΓœACB=90ΓψΘ§mΓΈACΘ§ΓύΓœA'BC=90ΓψΘ§ΓύcosΓœA'CB![]() Θ§ΓύΓœA'CB=30ΓψΘ§ΓύΓœACA'=60ΓψΘΜ
Θ§ΓύΓœA'CB=30ΓψΘ§ΓύΓœACA'=60ΓψΘΜ
Θ®2Θ©ΓΏMΈΣA'B'ΒΡ÷–ΒψΘ§ΓύΓœA'CM=ΓœMA'CΘ§”…–ΐΉΣΩ…ΒΟΘΚΓœMA'C=ΓœAΘ§ΓύΓœA=ΓœA'CMΘ§ΓύtanΓœPCB=tanΓœA![]() Θ§ΓύPB
Θ§ΓύPB![]() BC
BC![]() Θ°
Θ°
ΓΏΓœBQC=ΓœBCP=ΓœAΘ§ΓύtanΓœBQC=tanΓœA![]() Θ§ΓύBQ=BC
Θ§ΓύBQ=BC![]() 2Θ§ΓύPQ=PB+BQ
2Θ§ΓύPQ=PB+BQ![]() ΘΜ
ΘΜ
Θ®3Θ©ΓΏSΥΡ±Ώ–ΈPA'B'Q=SΓςPCQ©¹SΓςA'CB'=SΓςPCQ![]() Θ§ΓύSΥΡ±Ώ–ΈPA'B'QΉν–ΓΘ§Φ¥SΓςPCQΉν–ΓΘ§ΓύSΓςPCQ
Θ§ΓύSΥΡ±Ώ–ΈPA'B'QΉν–ΓΘ§Φ¥SΓςPCQΉν–ΓΘ§ΓύSΓςPCQ![]() PQΓΝBC
PQΓΝBC![]() PQΘ§
PQȧ
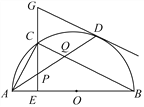
»ΓPQΒΡ÷–ΒψGΘ°
ΓΏΓœPCQ=90ΓψΘ§ΓύCG![]() PQΘ§Φ¥PQ=2CGΘ§Β±CGΉν–Γ ±Θ§PQΉν–ΓΘ§ΓύCGΓΆPQΘ§Φ¥CG”κCB÷ΊΚœ ±Θ§CGΉν–ΓΘ§ΓύCGmin
PQΘ§Φ¥PQ=2CGΘ§Β±CGΉν–Γ ±Θ§PQΉν–ΓΘ§ΓύCGΓΆPQΘ§Φ¥CG”κCB÷ΊΚœ ±Θ§CGΉν–ΓΘ§ΓύCGmin![]() Θ§PQmin=2
Θ§PQmin=2![]() Θ§ΓύSΓςPCQΒΡΉν–Γ÷Β=3Θ§SΥΡ±Ώ–ΈPA'B'Q=3
Θ§ΓύSΓςPCQΒΡΉν–Γ÷Β=3Θ§SΥΡ±Ώ–ΈPA'B'Q=3![]() ΘΜ
ΘΜ