题目内容
【题目】平面直角坐标系![]() 中,对称轴平行与
中,对称轴平行与![]() 轴的抛物线过点
轴的抛物线过点![]() 、
、![]() 和
和![]() .
.
(![]() )求抛物线的表达式.
)求抛物线的表达式.
(![]() )现将此抛物线先沿
)现将此抛物线先沿![]() 轴方向向右平移
轴方向向右平移![]() 个单位,再沿
个单位,再沿![]() 轴方向平移
轴方向平移![]() 个单位,若所得抛物线与
个单位,若所得抛物线与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左边),且使
的左边),且使![]() (顶点
(顶点![]() 、
、![]() 、
、![]() 依次对应顶点
依次对应顶点![]() 、
、![]() 、
、![]() ),试求
),试求![]() 的值,并说明方向.
的值,并说明方向.

【答案】(1)![]() ;(2)6
;(2)6
【解析】试题分析:(1)利用待定系数法直接求出抛物线的解析式;
(2)设出D,E坐标,根据平移,用k表示出平移后的抛物线解析式,利用坐标轴上点的特点得出m+n=16,mn=63-![]() ,进而利用相似三角形得出比例式建立方程即可求出k
,进而利用相似三角形得出比例式建立方程即可求出k
试题解析:(![]() )设的物线
)设的物线![]() .
.
将点![]() ,
, ![]() 和
和![]() 代入得:
代入得:
 解得:
解得: 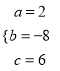 .
.
∴![]() .
.
(![]() )设点
)设点![]() ,
, ![]() .
.
∵![]() ,∴
,∴ ![]() ,
, ![]() .
.
由(![]() )知,抛物线的解析式为
)知,抛物线的解析式为![]() .
.
∴将此抛物线先沿![]() 轴方向向右平移
轴方向向右平移![]() 个单位,得到
个单位,得到![]() ,
,
即![]() .
.
∴再沿![]() 轴方向平移
轴方向平移![]() 个单位,则
个单位,则![]() ;
;
令![]() ,则
,则![]() ,
,
∴![]() .
.
∴![]() ,
, ![]() (韦达定理).
(韦达定理).
∵![]() ,
, ![]() ,
,
∴![]() .
.
∵![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∴k=6,
即:k=6,向下平移6个单位.

练习册系列答案
相关题目
【题目】某校为了了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四个等级,并绘制成下面的频数分布表(表一)和扇形统计图(图①)。
表一
等级 | 成绩(得分) | 频数(人数) | 频率 |
A | 10分 | 7 | 0.14 |
9分 | 12 | 0.24 | |
B | 8分 |
|
|
7分 | 8 | 0.16 | |
C | 6分 |
|
|
5分 | 1 | 0.02 | |
D | 5分以下 | 3 | 0.06 |
合计 | 50 | 1.00 |

(1)求出![]() 、
、![]() 的值,直接写出
的值,直接写出![]() 、
、![]() 的值;
的值;
(2)求表示得分为C等级的扇形的圆心角的度数;
(3)如果该校九年级共有男生250名,试估计这250名男生中成绩达到A等级的人数约有多少人?
