题目内容
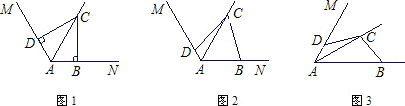
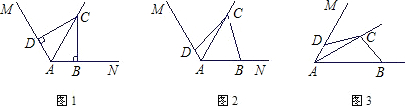
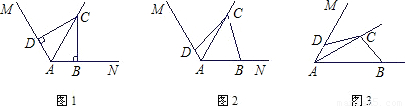
已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG,当点E在线段BC上时(如图1)易证:AB=CG+CE.当点在E线段BC的延长线上时(如图2),猜想AB、CG、CE之间的关系并证明;当点在E线段CB的延长线上时(如图3),猜想AB、CG、CE之间的关系.

(1)AB=CG-CE
证明:∵AC是菱形ABCD的对角线且∠BAC=60°,
∴AC=AD.
∵四边形AEFG菱形,
∴.
∵∠DAC=∠GAE=60°,
∴∠DAG=∠CAE.
在△ACE和△ADG中 ,
,
∴△ACE≌△ADG(SAS),
∴CE=DG.
∴AB=CD=CG-DG=CG-CE;
(2)AB=CE-CG.
同理可证△ACG≌△ABE,
∴BE=CG.
∴AB=CB=CE-BE=CE-CG.
分析:(1)根据菱形的性质可得AC=AD,AE=AG,然后证明∠DAG=∠CAE,可利用SAS证明△ACE≌△ADG,根据全等三角形的性质可得CE=DG,再根据线段的和差关系和等量代换可得答案;
(2)方法与(1)类似可证明△ACG≌△ABE,进而得到BE=CG,然后可得AB=CE-CG.
点评:此题主要考查了菱形的性质,以及等边三角形的性质,关键是掌握菱形的四边相等.
证明:∵AC是菱形ABCD的对角线且∠BAC=60°,
∴AC=AD.
∵四边形AEFG菱形,
∴.
∵∠DAC=∠GAE=60°,

∴∠DAG=∠CAE.
在△ACE和△ADG中
 ,
,∴△ACE≌△ADG(SAS),
∴CE=DG.
∴AB=CD=CG-DG=CG-CE;
(2)AB=CE-CG.
同理可证△ACG≌△ABE,
∴BE=CG.
∴AB=CB=CE-BE=CE-CG.
分析:(1)根据菱形的性质可得AC=AD,AE=AG,然后证明∠DAG=∠CAE,可利用SAS证明△ACE≌△ADG,根据全等三角形的性质可得CE=DG,再根据线段的和差关系和等量代换可得答案;
(2)方法与(1)类似可证明△ACG≌△ABE,进而得到BE=CG,然后可得AB=CE-CG.
点评:此题主要考查了菱形的性质,以及等边三角形的性质,关键是掌握菱形的四边相等.

练习册系列答案
相关题目
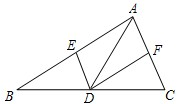 22、如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.
22、如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F. (2013•金山区二模)如图,已知在等腰三角形△ABC中,AB=AC,BO是AC边上的中线,延长BO至D,使得DO=BO;延长BA至E,使AE=AB,联结CD、DE,在AE取一点P,联结DP,并延长DP、CA交于点G.求证:
(2013•金山区二模)如图,已知在等腰三角形△ABC中,AB=AC,BO是AC边上的中线,延长BO至D,使得DO=BO;延长BA至E,使AE=AB,联结CD、DE,在AE取一点P,联结DP,并延长DP、CA交于点G.求证: