��Ŀ����
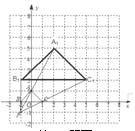
��ͼ����ƽ��ֱ������ϵ�У���A��B��C��P������ֱ�Ϊ��0��1����
����1��0������1��0��������1����1����
С��1:��A��B��C����������ߵı���ʽ��
С��2:��PΪλ�����ģ�����ABC�Ŵ�ʹ�÷Ŵ��ġ�A1B1C1���OAB��Ӧ�߶εı�Ϊ3��1��������ͼ�����л����Ŵ��ġ�A1B1C1����������A1B1C1���ABC�ڵ�Pͬ�ࣩ��
С��3:����A1��B1��C1������������ܷ��ɣ�1���е�������ƽ�Ƶõ�����˵�����ɡ�
����1��0������1��0��������1����1����
С��1:��A��B��C����������ߵı���ʽ��
С��2:��PΪλ�����ģ�����ABC�Ŵ�ʹ�÷Ŵ��ġ�A1B1C1���OAB��Ӧ�߶εı�Ϊ3��1��������ͼ�����л����Ŵ��ġ�A1B1C1����������A1B1C1���ABC�ڵ�Pͬ�ࣩ��
С��3:����A1��B1��C1������������ܷ��ɣ�1���е�������ƽ�Ƶõ�����˵�����ɡ�

��1:
�辭��A��B��C����������ߵı���ʽy=a(x��1)��x+1)��
�߾�����0��1)�� ��1=a(��1)��1
��a=��1����y=��1��(x��1) (x+1)=��x2+1��
С��2:��ͼ��ʾ
��3:
�辭��A1��B1��C1�����������Ϊ��y=a(x��2)2+5��
��(5��2)����ɵ�a=��13 ��y=��13(x��2)2+5
�ߺͣ�1���õ��Ķ�����ϵ����ͬ ���ͨ��ƽ�Ƶ�
��1���������Ӧ��������ʽ���ѵ�A���������⼴�ɣ�
��2������PA���ӳ���ʹPA1=3PA��ͬ���õ�������㣬˳�����Ӽ��ɣ�
��3���õ�������ĺ�������ʽ����������ϵ���Ƿ���ȣ���ȼ���ͨ��ƽ�Ƶõ���
�⣺��1���辭��A��B��C����������ߵı���ʽy=a��x-1����x+1����
�߾�����0��1����
��1=a��-1����1��
��a=-1��
��y=-1����x-1����x+1��=-x2+1��
��2����ͼ��ʾ��
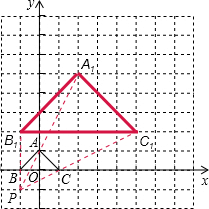
��3���辭��A1��B1��C1�����������Ϊy=a��x-2��2+5��
�ѣ�5��2������ɵ�a=-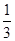 ��
��
��y=-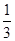 ��x-2��2+5��
��x-2��2+5��
�ߺͣ�1���õ��Ķ�����ϵ����ͬ��
���ͨ��ƽ�Ƶõ���
��2������PA���ӳ���ʹPA1=3PA��ͬ���õ�������㣬˳�����Ӽ��ɣ�
��3���õ�������ĺ�������ʽ����������ϵ���Ƿ���ȣ���ȼ���ͨ��ƽ�Ƶõ���
�⣺��1���辭��A��B��C����������ߵı���ʽy=a��x-1����x+1����
�߾�����0��1����
��1=a��-1����1��
��a=-1��
��y=-1����x-1����x+1��=-x2+1��
��2����ͼ��ʾ��

��3���辭��A1��B1��C1�����������Ϊy=a��x-2��2+5��
�ѣ�5��2������ɵ�a=-
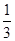 ��
����y=-
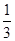 ��x-2��2+5��
��x-2��2+5���ߺͣ�1���õ��Ķ�����ϵ����ͬ��
���ͨ��ƽ�Ƶõ���

��ϰ��ϵ�д�
�����Ŀ

 ���õ�ʣ���̵����Ϊ
���õ�ʣ���̵����Ϊ ����. ������ͼ����, ����ȷ��ӳ
����. ������ͼ����, ����ȷ��ӳ

 =0���� ��P��x,y����ֱ������ϵ�У� ��
=0���� ��P��x,y����ֱ������ϵ�У� ��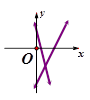
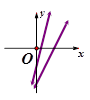
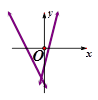
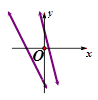
 ��ͬһֱ������ϵ�е�ͼ������ǣ�������
��ͬһֱ������ϵ�е�ͼ������ǣ�������



