题目内容
已知关于x的一元二次方程ax2+bx+c=0没有实数解.甲由于看错了二次项系数,误求得两根为2和4;乙由于看错了某一项系数的符号,误求得两根为-1和4,那么, =________.
=________.
-6
分析:先利用两根分别表示出错误的方程为:甲,设k(x-2)(x-4)=0得kx2-6kx+8k=0;乙,设p(x+1)(x-4)=0得px2-3px-4p=0,无论怎么错误,甲和乙的方程里面常量相同,就是8k=-4p,即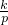 =-
=- ,把第一个方程中的一次项和常数项,第二个方程中的二次项代入所求代数式中化简后可解.
,把第一个方程中的一次项和常数项,第二个方程中的二次项代入所求代数式中化简后可解.
解答:对于甲:设k(x-2)(x-4)=0
得kx2-6kx+8k=0.
对于乙:设p(x+1)(x-4)=0
得px2-3px-4p=0
从这两个方程可看出:无论怎么错误,甲和乙的方程里面常量相等,
所以8k=-4p,即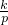 =-
=- ,p=-2k,
,p=-2k,
则 =
= =-6.
=-6.
故答案为:-6.
点评:此题考查了一元二次方程的特点,以及方程之间的关系,难度不小.需要利用方程的两根来表示出两个错误的方程,并通过比较后,得出初步判断为无论怎么错误,甲和乙的方程里面常量相等这个关键的等量关系,然后通过等量代换求解.
分析:先利用两根分别表示出错误的方程为:甲,设k(x-2)(x-4)=0得kx2-6kx+8k=0;乙,设p(x+1)(x-4)=0得px2-3px-4p=0,无论怎么错误,甲和乙的方程里面常量相同,就是8k=-4p,即
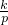 =-
=- ,把第一个方程中的一次项和常数项,第二个方程中的二次项代入所求代数式中化简后可解.
,把第一个方程中的一次项和常数项,第二个方程中的二次项代入所求代数式中化简后可解.解答:对于甲:设k(x-2)(x-4)=0
得kx2-6kx+8k=0.
对于乙:设p(x+1)(x-4)=0
得px2-3px-4p=0
从这两个方程可看出:无论怎么错误,甲和乙的方程里面常量相等,
所以8k=-4p,即
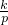 =-
=- ,p=-2k,
,p=-2k,则
 =
= =-6.
=-6.故答案为:-6.
点评:此题考查了一元二次方程的特点,以及方程之间的关系,难度不小.需要利用方程的两根来表示出两个错误的方程,并通过比较后,得出初步判断为无论怎么错误,甲和乙的方程里面常量相等这个关键的等量关系,然后通过等量代换求解.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知关于x的一元二次x2-6x+k+1=0的两个实数根x1,x2,
+
=1,则k的值是( )
| 1 |
| x1 |
| 1 |
| x2 |
| A、8 | B、-7 | C、6 | D、5 |
 .
. .
.