��Ŀ����
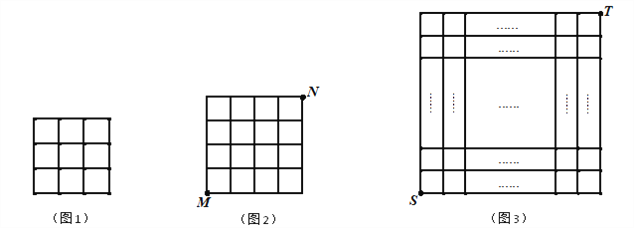
����Ŀ����ÿ��С�����εı߳�Ϊ1�������У�ÿ��С�����εĶ����Ϊ��㣮���ǽ���һ������ƶ�����֮���![]() ����һ�������˶���Ϊһ�������任��
����һ�������˶���Ϊһ�������任��
��1����ͼ1�л����߳�Ϊ![]() �������Σ�ʹ���Ķ���������ĸ���ϣ�
�������Σ�ʹ���Ķ���������ĸ���ϣ�
��2����ͼ2����һֻ����С���Ӹ��![]() ���������������任����������Եĸ��
���������������任����������Եĸ��![]() ����������Ҫ�����任�Ĵ����� �Σ�
����������Ҫ�����任�Ĵ����� �Σ�
��3����ͼ3����![]() �������������У�һֻ����С���Ӹ��
�������������У�һֻ����С���Ӹ��![]() �������ɴ������任����������Եĸ��
�������ɴ������任����������Եĸ��![]() ���������������·��Ϊ ��
���������������·��Ϊ ��
���𰸡���1����ͼ����������2��4����3��14![]()
�������������������1��.�������⻭��ͼ�μ��ɣ���2��.�������⻭��ͼ�ν�𣻣�3�����ݴ�һ������ƶ�����֮���![]() ����һ�������˶���Ϊһ�������任,�������A-C-F�ķ��������任10�κ��S��λ��,�ٸ��ݵ�T��λ�ý����ʵ��ı任,���ɵõ��任�ܴ���.
����һ�������˶���Ϊһ�������任,�������A-C-F�ķ��������任10�κ��S��λ��,�ٸ��ݵ�T��λ�ý����ʵ��ı任,���ɵõ��任�ܴ���.
�⣺��1����ͼ1��
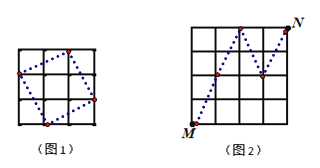
��2����ͼ2��������Ҫ�����任�Ĵ�����4��.
��3����ͼ3, ![]() ,
,
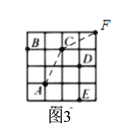
![]() ���α任�൱�������ƶ�3��,�����ƶ�3��,
���α任�൱�������ƶ�3��,�����ƶ�3��,
����![]() ,
,
![]() (��������)��
(��������)��
![]() ��A-C-F�ķ��������任10�κ�,�൱�������ƶ���10��2��3=15��,�����ƶ���10��2��3=15��,��ʱSλ����ͼ��ʾ��5��5������������ĵ�G��,�ٰ���ͼ��ʾ�ķ�ʽ�任4�μ��ɵ����T��,
��A-C-F�ķ��������任10�κ�,�൱�������ƶ���10��2��3=15��,�����ƶ���10��2��3=15��,��ʱSλ����ͼ��ʾ��5��5������������ĵ�G��,�ٰ���ͼ��ʾ�ķ�ʽ�任4�μ��ɵ����T��,
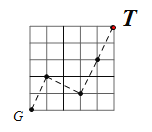
![]() �Ӹ������εĶ���S���������任����������ԵĶ���T,������Ҫ�����任�Ĵ�����14��,
�Ӹ������εĶ���S���������任����������ԵĶ���T,������Ҫ�����任�Ĵ�����14��,
�������������·��Ϊ![]() .
.