题目内容
 如图,CD为⊙O的直径,弦AB⊥CD于P,AB=8cm,OP=3cm,则⊙O的半径为________cm.
如图,CD为⊙O的直径,弦AB⊥CD于P,AB=8cm,OP=3cm,则⊙O的半径为________cm.
5
分析:连接OA,因为直径CD⊥AB,由垂径定理得到AP=BP,而AB=8cm,在Rt△OAP中,OP=3cm,利用勾股定理即可求出OA.
解答: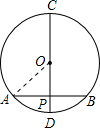 解:连接OA,如图,
解:连接OA,如图,
∵直径CD⊥AB,
∴AP=BP,
而AB=8cm,
∴AP=4cm,
在Rt△OAP中,OP=3cm,OA2=OP2+AP2,
∴OA=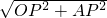 =5.
=5.
即⊙O的半径为5cm.
故答案为5.
点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理.
分析:连接OA,因为直径CD⊥AB,由垂径定理得到AP=BP,而AB=8cm,在Rt△OAP中,OP=3cm,利用勾股定理即可求出OA.
解答:
 解:连接OA,如图,
解:连接OA,如图,∵直径CD⊥AB,
∴AP=BP,
而AB=8cm,
∴AP=4cm,
在Rt△OAP中,OP=3cm,OA2=OP2+AP2,
∴OA=
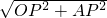 =5.
=5.即⊙O的半径为5cm.
故答案为5.
点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理.

练习册系列答案
相关题目
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )| A、1cm | B、2cm | C、3cm | D、4cm |


 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为