题目内容
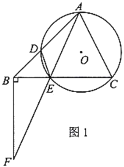
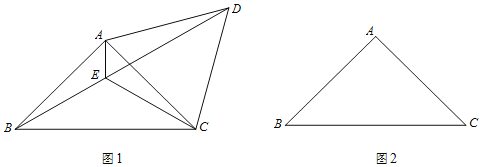
【题目】在学习了矩形后,数学活动小组开展了探究活动.如图1,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,先以
上,先以![]() 为折痕将
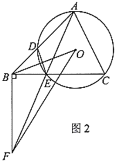
为折痕将![]() 点往右折,如图2所示,再过点
点往右折,如图2所示,再过点![]() 作
作![]() ,垂足为
,垂足为![]() ,如图3所示.
,如图3所示.
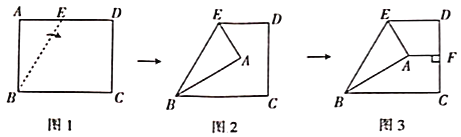
(1)在图3中,若![]() ,则
,则![]() 的度数为______,
的度数为______,![]() 的长度为______.
的长度为______.
(2)在(1)的条件下,求![]() 的长.
的长.
(3)在图3中,若![]() ,则
,则![]() ______.
______.
【答案】(1)![]() ,4;(2)2;(3)
,4;(2)2;(3)![]()
【解析】
(1)根据矩形的性质得出![]() ,可以推出
,可以推出![]() ,再根据折叠的性质即可得出答案;设AE=x,则BE=2x,再根据勾股定理即可得出AE的值.
,再根据折叠的性质即可得出答案;设AE=x,则BE=2x,再根据勾股定理即可得出AE的值.
(2)作![]() 交
交![]() 于点
于点![]() ,在
,在![]() 中根据余弦得出BG,从而得出CG,再证明四边形
中根据余弦得出BG,从而得出CG,再证明四边形![]() 是矩形即可得出答案;
是矩形即可得出答案;
(3)根据![]() 可得AG的值,从而推出BG的值,再根据线段的和与差即可得出答案.
可得AG的值,从而推出BG的值,再根据线段的和与差即可得出答案.
(1)![]() 四边形ABCD为矩形
四边形ABCD为矩形
![]() ,
,
![]()
![]()
![]()
![]()
![]()
设AE=x,则BE=2x
在![]() 中,根据勾股定理
中,根据勾股定理![]()
即![]()
解得![]() ,
,![]() (舍去)
(舍去)
![]()
![]() 的长度为4.
的长度为4.
故答案为:![]() ,4.
,4.
(2)如图,作![]() 交
交![]() 于点
于点![]() ,
,
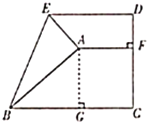
由(1)知![]() .
.
在![]() 中,
中,
∵![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() .
.
(3)![]()
![]()
![]()
![]()
![]()
![]()

练习册系列答案
相关题目
【题目】从甲地到乙地有A,B,C三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
线路 公交车用时的频数 公交车用时 | 30<t ≤35 | 35<t ≤40 | 40<t ≤45 | 45<t ≤50 | 合计 |
A | 59 | 151 | a | 124 | 500 |
B | 50 | b | 122 | 278 | 500 |
C | 45 | 265 | 167 | c | 500 |
(1)将上面表格补充完整;
(2)某天王先生和李女士从甲地到乙地,试用树状图或列表法求在早高峰期间两人刚好乘坐同一条线路的概率;
(3)小张从甲地到乙地,早高峰期间用时不超过45分钟,请问小张应该选择哪条线路?请说明理由.