题目内容
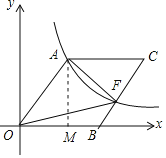
【题目】已知:如图四边形OACB是菱形,OB在X轴的正半轴上,sin∠AOB=![]() .反比例函数y=
.反比例函数y=![]() 在第一象限图象经过点A,与BC交于点F.S△AOF=
在第一象限图象经过点A,与BC交于点F.S△AOF=![]() ,则k=( )
,则k=( )

A. 15 B. 13 C. 12 D. 5
【答案】A
【解析】
过点A作AM⊥x轴于点M,设OA=a,通过解直角三角形找出点A的坐标,再根据四边形OACB是菱形、点F在边BC上,即可得出S△AOF=S菱形OBCA,结合菱形的面积公式即可得出a的值,进而依据点A的坐标得到k的值.
过点A作AM⊥x轴于点M,如图所示.
设OA=a=OB,则,
在Rt△OAM中,∠AMO=90°,OA=a,sin∠AOB=![]() ,
,
∴AM=OAsin∠AOB=![]() a,OM=
a,OM=![]() a,
a,
∴点A的坐标为(![]() a,
a,![]() a).
a).
∵四边形OACB是菱形,S△AOF=![]() ,
,
∴![]() OB×AM=
OB×AM=![]() ,
,
即![]() ×a×
×a×![]() a=39,
a=39,
解得a=±![]() ,而a>0,
,而a>0,
∴a=![]() ,即A(
,即A(![]() ,6),
,6),
∵点A在反比例函数y=![]() 的图象上,
的图象上,
∴k=![]() ×6=15.
×6=15.
故选A.
【解答】
解:

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目