Question

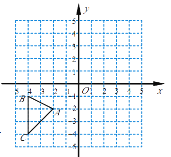
【题目】已知A、B两点的坐标分别为 （0，3），（2，0），以线段AB为直角边，在第一象限内作等腰直角三角形ABC，使∠BAC＝90°，如果在第二象限内有一点P（a，），且△ABP和△ABC的面积相等，则a＝_____．

Answer 1

【答案】-．

【解析】

先根据AB两点的坐标求出OA、OB的值，再由勾股定理求出AB的长度，根据三角形的面积公式即可得出△ABC的面积；连接OP，过点P作PE⊥x轴，由△ABP的面积与△ABC的面积相等，可知S△ABP＝S△POA+S△AOB﹣S△BOP＝，故可得出a的值．

∵A、B两点的坐标分别为 （0，3），（2，0），

∴OA＝3，OB＝2，

∴，

∵△ABC是等腰直角三角形，∠BAC＝90°，

∴，

作PE⊥x轴于E，连接OP，

此时BE＝2﹣a，

∵△ABP的面积与△ABC的面积相等，

∴，

，

解得a＝﹣．

故答案为﹣．