题目内容
 如图,已知一次函数y=2x+4的图象与x轴、y轴分别交于点A、B,且BC∥AO,梯形AOBC的面积为10.
如图,已知一次函数y=2x+4的图象与x轴、y轴分别交于点A、B,且BC∥AO,梯形AOBC的面积为10.(1)求点A、B、C的坐标;
(2)求直线AC的表达式.
分析:(1)根据一次函数解析式求得点A、B的坐标;然后根据梯形AOBC的面积公式来求点C的坐标;
(2)设直线AC的表达式为y=kx+b(k≠0).把点A、C的坐标分别代入函数解析式,列出关于k、b的二元一次方程组,通过解方程组即可求得k、b的值.
(2)设直线AC的表达式为y=kx+b(k≠0).把点A、C的坐标分别代入函数解析式,列出关于k、b的二元一次方程组,通过解方程组即可求得k、b的值.
解答:解:(1)由已知,A(-2,0),B(0,4).
所以OA=2,OB=4,
∵梯形AOBC的面积为10,∴
(OA+BC)-OB=10.
解得BC=3,所以点C(-3,4);
(2)设直线AC的表达式为y=kx+b(k≠0).
则
,解得
.
∴直线AC的表达式为y=-4x-8.
所以OA=2,OB=4,
∵梯形AOBC的面积为10,∴
| 1 |
| 2 |
解得BC=3,所以点C(-3,4);
(2)设直线AC的表达式为y=kx+b(k≠0).
则
|
|
∴直线AC的表达式为y=-4x-8.
点评:本题考查了待定系数法求一次函数的解析式.先根据条件列出关于字母系数的方程组,解方程组求解即可得到函数解析式.当已知函数解析式时,求函数中字母的值就是求关于字母系数的方程的解.

练习册系列答案
相关题目
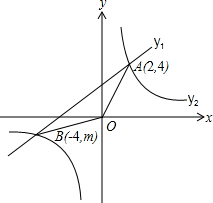 B(-4,m)两点.
B(-4,m)两点. 如图,已知一次函数y=kx+b的图象与反比例函数y=-
如图,已知一次函数y=kx+b的图象与反比例函数y=- (2013•新疆)如图,已知一次函数y1=kx+b与反比例函数
(2013•新疆)如图,已知一次函数y1=kx+b与反比例函数 如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数
如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数 如图,已知一次函数y=kx+b的图象交反比例函数
如图,已知一次函数y=kx+b的图象交反比例函数