题目内容
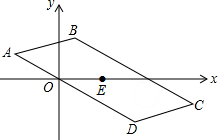 如图,平面直角坐标系中,平行四边形ABCD的中心E的坐标为(2,0),若点A的坐标为(-2,1),则点C的坐标为
如图,平面直角坐标系中,平行四边形ABCD的中心E的坐标为(2,0),若点A的坐标为(-2,1),则点C的坐标为
- A.(4,-1)
- B.(6,-1)
- C.(8,-1)
- D.(6,-2)
B
分析:首先连接AC,过点A作AG⊥x轴于点G,过点C作CH⊥x轴于点H,可得E是平行四边形ABCD的中心,即可得AC过点E,易证得△AEG≌△CEH,继而求得答案.
解答: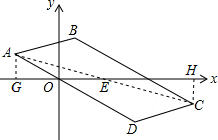 解:连接AC,过点A作AG⊥x轴于点G,过点C作CH⊥x轴于点H,
解:连接AC,过点A作AG⊥x轴于点G,过点C作CH⊥x轴于点H,
∵E是平行四边形ABCD的中心,
∴AC过点E,
∴AE=CE,
在△AEG和△CEH中,
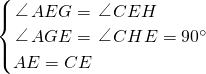 ,
,
∴△AEG≌△CEH(AAS),
∴EG=EH,CH=AG,
∵E的坐标为(2,0),点A的坐标为(-2,1),
∴EH=EG=4,CH=AG=1,
∴OH=OE+EH=6,
∴点C的坐标为:(6,-1).
故选B.
点评:此题考查了平行四边形的性质以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
分析:首先连接AC,过点A作AG⊥x轴于点G,过点C作CH⊥x轴于点H,可得E是平行四边形ABCD的中心,即可得AC过点E,易证得△AEG≌△CEH,继而求得答案.
解答:
 解:连接AC,过点A作AG⊥x轴于点G,过点C作CH⊥x轴于点H,
解:连接AC,过点A作AG⊥x轴于点G,过点C作CH⊥x轴于点H,∵E是平行四边形ABCD的中心,
∴AC过点E,
∴AE=CE,
在△AEG和△CEH中,
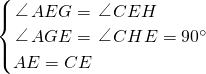 ,
,∴△AEG≌△CEH(AAS),
∴EG=EH,CH=AG,
∵E的坐标为(2,0),点A的坐标为(-2,1),
∴EH=EG=4,CH=AG=1,
∴OH=OE+EH=6,
∴点C的坐标为:(6,-1).
故选B.
点评:此题考查了平行四边形的性质以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案
相关题目
 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线 =2
=2 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.