题目内容
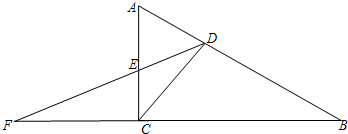
（2013•奉贤区一模）如图，已知在Rt△ABC中，∠ACB=90°，CD⊥AB于D，E是AC的中点，DE的延长线与BC的延长线交于点F．
（1）求证：△FDC∽△FBD；
（2）求证：
=
．
（1）求证：△FDC∽△FBD；
（2）求证：
| DF |
| BF |
| AC |
| BC |
分析：（1）根据直角三角形斜边上中线性质求出DE=EC，推出∠EDC=∠ECD，求出∠FDC=∠B，根据∠F=∠F证△FBD∽△FDC，即可；
（2）由（1）可知FBD∽△FDC，所以
=
，由已知条件可证明△BDC∽△BCA所以
=
即
=
．
（2）由（1）可知FBD∽△FDC，所以
| DF |
| BF |
| DC |
| BD |
| DC |
| BD |
| AC |
| BC |
| DF |
| BF |
| AC |
| BC |
解答：（1）证明：∵CD⊥AB，
∴∠ADC=90°，
∵E是AC的中点，
∴DE=EC，
∴∠EDC=∠ECD，
∵∠ACB=90°，∠BDC=90°
∴∠ECD+∠DCB=90°，∠DCB+∠B=90°，
∴∠ECD=∠B，
∴∠FDC=∠B，
∵∠F=∠F，
∴△FBD∽△FDC；
（2）∵△FBD∽△FDC，
∴
=
，
∵△BDC∽△BCA，
∴
=
，
∴
=
．
∴∠ADC=90°，
∵E是AC的中点，
∴DE=EC，
∴∠EDC=∠ECD，
∵∠ACB=90°，∠BDC=90°
∴∠ECD+∠DCB=90°，∠DCB+∠B=90°，
∴∠ECD=∠B，
∴∠FDC=∠B，
∵∠F=∠F，
∴△FBD∽△FDC；
（2）∵△FBD∽△FDC，
∴
| DF |
| BF |
| DC |
| BD |
∵△BDC∽△BCA，
∴
| DC |
| BD |
| AC |
| BC |
∴
| DF |
| BF |
| AC |
| BC |
点评：本题考查了相似三角形的判定和性质以及直角三角形斜边上的中线等于斜边的一半，解题的关键是由相似得到比例式．
练习册系列答案
相关题目
（2013•奉贤区一模）在Rt△ABC中，∠C=90°，AB=5，BC=3，点D、E分别在BC、AC上，且BD=CE，设点C关于DE的对称点为F，若DF∥AB，则BD的长为