Question

已知，如图：在△ABC中，∠ABC = 70°，∠ACB = 50°，E分别为AC、AB上的点，且BE = CD，G、M、N分别为BC、BD、CE的中点。
(1) 求∠MGN与∠A的度数相等吗？说明理由。
(2) 判断△GMN的形状，说明理由。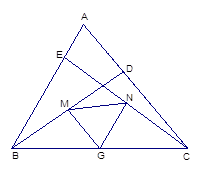

Answer 1

（1）相等；
∵G、M、N分别为BC、BD、CE的中点，
∴GM∥CD，GN∥BE，
∴∠BGM=∠ACB=50°，∠CGN=∠ABC=70°，
∴∠MGN=180°-∠BGM-∠CGN=60°，
已知∠ABC=70°，∠ACB=50°，
∴∠A=180°-∠ABC-∠ACB=60°，
∴∠MGN=∠A；
（2）等边三角形；
∵G、M、N分别为BC、BD、CE的中点，
∴GM=CD，GN=BE，
又已知BE=CD，
∴GM=GN，
∴∠GMN=∠CNM，
又∵∠MGN=60°，
∴∠GMN=∠CNM=（180°-60°）=60°，
∴∠GMN=∠CNM=∠MGN=60°，
∴△GMN为等边三角形．

解析