题目内容
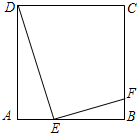 如图所示,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
如图所示,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.(1)求证:△ADE∽△BEF;
(2)设正方形的边长为8,AE=x,BF=y,求y与x的函数关系式,并求自变量x的取值范围.
分析:(1)由条件可以得出∠A=∠B,∠AED=∠EBF,从而得出△ADE∽△BEF;
(2)由(1)的结论可以得出
=
,然后将AE=x,BF=y的值代入等式就可以表示出y的代数式.自变量的取值范围为:0<x<8.
(2)由(1)的结论可以得出
| AE |
| BF |
| AD |
| BE |
解答:解:(1)∵ABCD是正方形,
∴∠DAE=∠EBF=90°,AD=AB,
∴∠ADE+∠DEA=90°,
∵EF⊥DE,
∴∠AED+∠FEB=90°,
∴∠ADE=∠FEB,
∴△ADE∽△BEF;
(2)∵△ADE∽△BEF,
∴
=
.
∵AD=AB=8,
∴BE=8-x,
∴
=
∴y=-
x2+x.
自变量x的取值范围是(0<x<8).
∴∠DAE=∠EBF=90°,AD=AB,
∴∠ADE+∠DEA=90°,
∵EF⊥DE,
∴∠AED+∠FEB=90°,
∴∠ADE=∠FEB,
∴△ADE∽△BEF;
(2)∵△ADE∽△BEF,
∴
| AE |
| BF |
| AD |
| BE |
∵AD=AB=8,
∴BE=8-x,
∴
| x |
| y |
| 8 |
| 8-x |
∴y=-
| 1 |
| 8 |
自变量x的取值范围是(0<x<8).
点评:本题考查了正方形的性质,直角三角形的性质,相似三角形的判定与性质的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 23、如图所示,E是正方形ABCD的边CD上一点,将△AED绕点A顺时针旋转90°,得到△AFB,则AE与AF有何关系?试说明理由.
23、如图所示,E是正方形ABCD的边CD上一点,将△AED绕点A顺时针旋转90°,得到△AFB,则AE与AF有何关系?试说明理由. 18、如图所示,ABCD是正方形,BE⊥BF,BE=BF,试判断AE与FC的位置关系,并给出证明.
18、如图所示,ABCD是正方形,BE⊥BF,BE=BF,试判断AE与FC的位置关系,并给出证明. 如图所示,E是正方形ABCD的边BC延长线上的点,且BC=CE.
如图所示,E是正方形ABCD的边BC延长线上的点,且BC=CE.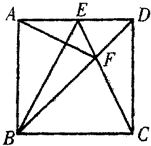 23、如图所示,E是正方形ABCD中AD边上的中点,BD与CE交于点F.请你根据图形判断AF与BE的位置具有什么关系?并给予证明.
23、如图所示,E是正方形ABCD中AD边上的中点,BD与CE交于点F.请你根据图形判断AF与BE的位置具有什么关系?并给予证明. 如图所示,P是正方形ABCD的边CD上一点,∠BAP的角平分线交BC于Q,
如图所示,P是正方形ABCD的边CD上一点,∠BAP的角平分线交BC于Q,