ΧβΡΩΡΎ»ί
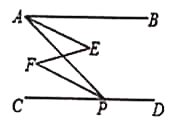
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§ΫΪΝΫΗωΆξ»ΪœύΆ§ΒΡ»ΐΫ«–Έ÷ΫΤ§ABCΚΆDEC÷ΊΚœΖ≈÷ΟΘ§Τδ÷–![]() Θ§
Θ§![]() .
.
Θ®1Θ©≤ΌΉςΖΔœ÷
ΔΌΙΧΕ®![]() Θ§ Ι
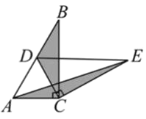
Θ§ Ι![]() »ΤΒψC–ΐΉΣ.Β±ΒψD«ΓΚΟ¬δ‘ΎAB±Ώ…œ ±Θ®»γΆΦ2Θ©ΘΜœΏΕΈDE”κACΒΡΈΜ÷ΟΙΊœΒ «________Θ§«κ÷ΛΟςΘΜ
»ΤΒψC–ΐΉΣ.Β±ΒψD«ΓΚΟ¬δ‘ΎAB±Ώ…œ ±Θ®»γΆΦ2Θ©ΘΜœΏΕΈDE”κACΒΡΈΜ÷ΟΙΊœΒ «________Θ§«κ÷ΛΟςΘΜ
ΔΎ…η![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() Θ§
Θ§![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() Θ§‘ρ
Θ§‘ρ![]() ”κ
”κ![]() ΒΡ ΐΝΩΙΊœΒ «________.
ΒΡ ΐΝΩΙΊœΒ «________.
Θ®2Θ©≤¬œκ¬έ÷Λ
Β±![]() »ΤΒψC–ΐΉΣΒΫΆΦ3Υυ ΨΒΡΈΜ÷Ο ±Θ§–ΓΟς≤¬œκΘ®1Θ©÷–
»ΤΒψC–ΐΉΣΒΫΆΦ3Υυ ΨΒΡΈΜ÷Ο ±Θ§–ΓΟς≤¬œκΘ®1Θ©÷–![]() ”κ
”κ![]() ΒΡ ΐΝΩΙΊœΒ»‘»Μ≥…ΝΔΘ§«κΡψΖ÷±πΉς≥ω
ΒΡ ΐΝΩΙΊœΒ»‘»Μ≥…ΝΔΘ§«κΡψΖ÷±πΉς≥ω![]() ΚΆ
ΚΆ![]() ÷–BCΓΔCE±Ώ…œΒΡΗΏΘ§≤Δ”…¥Υ÷ΛΟς–ΓΟςΒΡ≤¬œκ.
÷–BCΓΔCE±Ώ…œΒΡΗΏΘ§≤Δ”…¥Υ÷ΛΟς–ΓΟςΒΡ≤¬œκ.
Θ®3Θ©ΆΊ’ΙΧΫΨΩ
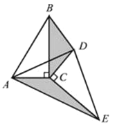
ΦΚ÷Σ![]() Θ§ΒψD «ΤδΫ«ΤΫΖ÷œΏ…œ“ΜΒψΘ§
Θ§ΒψD «ΤδΫ«ΤΫΖ÷œΏ…œ“ΜΒψΘ§![]() Θ§
Θ§![]() ΫΜBC”ΎΒψEΘ®»γΆΦ4Θ©Θ§«κΈ ‘Ύ…δœΏBA…œ «Ζώ¥φ‘ΎΒψFΘ§ Ι
ΫΜBC”ΎΒψEΘ®»γΆΦ4Θ©Θ§«κΈ ‘Ύ…δœΏBA…œ «Ζώ¥φ‘ΎΒψFΘ§ Ι![]() Θ§»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΖϊΚœΧθΦΰΒΡΒψFΒΡΗω ΐΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
Θ§»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΖϊΚœΧθΦΰΒΡΒψFΒΡΗω ΐΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
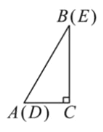
ΆΦ1 ΆΦ2
ΆΦ3 ΆΦ4
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() άμ”…ΦϊΫβΈωΘ§
άμ”…ΦϊΫβΈωΘ§![]() ΘΜΘ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©¥φ‘ΎΝΫΗω.
ΘΜΘ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©¥φ‘ΎΝΫΗω.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΔΌΗυΨί–ΐΉΣΒΡ–‘÷ Ω…ΒΟ![]() Θ§»ΜΚσ«σ≥ω
Θ§»ΜΚσ«σ≥ω![]() «Β»±Ώ»ΐΫ«–ΈΘ§ΗυΨίΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟ
«Β»±Ώ»ΐΫ«–ΈΘ§ΗυΨίΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟ![]() Θ§»ΜΚσΗυΨίΡΎ¥μΫ«œύΒ»Θ§ΝΫ÷±œΏΤΫ––Ϋβ¥πΘΜ
Θ§»ΜΚσΗυΨίΡΎ¥μΫ«œύΒ»Θ§ΝΫ÷±œΏΤΫ––Ϋβ¥πΘΜ
ΔΎΗυΨίΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟACΘΫADΘ§‘ΌΗυΨί÷±Ϋ«»ΐΫ«–Έ30ΓψΫ«ΥυΕ‘ΒΡ÷±Ϋ«±ΏΒ»”Ύ–±±ΏΒΡ“ΜΑκ«σ≥ωACΘΫ![]() ABΘ§»ΜΚσ«σ≥ωADΘΫBDΘ§‘ΌΗυΨίΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ «σ≥ωΒψCΒΫABΒΡΨύάκΒ»”ΎΒψDΒΫACΒΡΨύάκΘ§»ΜΚσΗυΨί»¹»ǿΒΡ»ΐΫ«–ΈΒΡΟφΜΐœύΒ»Ϋβ¥πΘΜ
ABΘ§»ΜΚσ«σ≥ωADΘΫBDΘ§‘ΌΗυΨίΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ «σ≥ωΒψCΒΫABΒΡΨύάκΒ»”ΎΒψDΒΫACΒΡΨύάκΘ§»ΜΚσΗυΨί»¹»ǿΒΡ»ΐΫ«–ΈΒΡΟφΜΐœύΒ»Ϋβ¥πΘΜ
Θ®2Θ©ΗυΨί–ΐΉΣΒΡ–‘÷ Ω…ΒΟBCΘΫCEΘ§ACΘΫCDΘ§‘Ό«σ≥ωΓœACNΘΫΓœDCMΘ§»ΜΚσάϊ”ΟΓΑΫ«Ϋ«±ΏΓ±÷ΛΟςΓςACNΚΆΓςDCM»ΪΒ»Θ§ΗυΨί»ΪΒ»»ΐΫ«–ΈΕ‘”Π±ΏœύΒ»Ω…ΒΟANΘΫDMΘ§»ΜΚσάϊ”Ο»¹»ǿΒΡ»ΐΫ«–ΈΒΡΟφΜΐœύΒ»÷ΛΟςΘ°
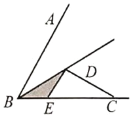
Θ®3Θ©ΙΐΒψDΉς![]() Θ§«σ≥ωΥΡ±Ώ–Έ
Θ§«σ≥ωΥΡ±Ώ–Έ![]() «Νβ–ΈΘ§ΗυΨίΝβ–ΈΒΡΕ‘±ΏœύΒ»Ω…ΒΟ
«Νβ–ΈΘ§ΗυΨίΝβ–ΈΒΡΕ‘±ΏœύΒ»Ω…ΒΟ![]() Θ§»ΜΚσΗυΨί»¹»ǿΒΡ»ΐΫ«–ΈΒΡΟφΜΐœύΒ»Ω…÷ΣΒψ
Θ§»ΜΚσΗυΨί»¹»ǿΒΡ»ΐΫ«–ΈΒΡΟφΜΐœύΒ»Ω…÷ΣΒψ![]() ΈΣΥυ«σΒΡΒψΘ§ΙΐΒψDΉς
ΈΣΥυ«σΒΡΒψΘ§ΙΐΒψDΉς![]() Θ§«σ≥ω
Θ§«σ≥ω![]() Θ§¥”ΕχΒΟΒΫ
Θ§¥”ΕχΒΟΒΫ![]() «Β»±Ώ»ΐΫ«–ΈΘ§»ΜΚσ«σ≥ω
«Β»±Ώ»ΐΫ«–ΈΘ§»ΜΚσ«σ≥ω![]() Θ§‘Ό«σ≥ω
Θ§‘Ό«σ≥ω![]() Θ§άϊ”ΟΓΑ±ΏΫ«±ΏΓ±÷ΛΟς
Θ§άϊ”ΟΓΑ±ΏΫ«±ΏΓ±÷ΛΟς![]() »ΪΒ»Θ§ΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡΟφΜΐœύΒ»Ω…ΒΟΒψ
»ΪΒ»Θ§ΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡΟφΜΐœύΒ»Ω…ΒΟΒψ![]() “≤ «Υυ«σΒΡΒψΘ°
“≤ «Υυ«σΒΡΒψΘ°
Θ®1Θ©ΔΌ![]() Θ§
Θ§
œ¬Οφ÷ΛΟςΘΚ”…Χβ“β![]() Θ§”÷”…–ΐΉΣΒΟ
Θ§”÷”…–ΐΉΣΒΟ![]() Θ§
Θ§
Υυ“‘![]() «Β»±Ώ»ΐΫ«–Έ.
«Β»±Ώ»ΐΫ«–Έ.
Υυ“‘![]() Θ§”Ύ «
Θ§”Ύ «![]() Θ§Υυ“‘
Θ§Υυ“‘![]() .
.
ΔΎΓΏACΘΫ![]() ABΘ§ADΘΫACΘ§
ABΘ§ADΘΫACΘ§
ΓύADΘΫBDΘ§
Γύ![]()
ÿDEøACȧ
Γύ![]() Θ§
Θ§
Γύ![]() .
.
Ι ¥πΑΗΈΣΘΚDEΓΈACΘ§![]() Θ°
Θ°
Θ®2Θ©»γΆΦΘ§
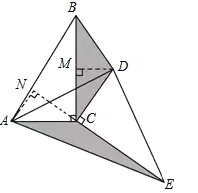
ΓΏΓςDEC «”…ΓςABC»ΤΒψC–ΐΉΣΒΟΒΫΘ§
ΓύBCΘΫCEΘ§ACΘΫCDΘ§
ΓΏΓœACNΘΪΓœBCNΘΫ90ΓψΘ§ΓœDCMΘΪΓœBCNΘΫ180Γψ90ΓψΘΫ90ΓψΘ§
ΓύΓœACNΘΫΓœDCMΘ§
‘Ύ![]() ΚΆ
ΚΆ![]() ÷–Θ§
÷–Θ§
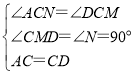 Θ§
Θ§
Γύ![]() Θ®AASΘ©Θ§
Θ®AASΘ©Θ§
ΓύANΘΫDMΘ§
ΓύΓςBDCΒΡΟφΜΐΚΆΓςAECΒΡΟφΜΐœύ»Ȯ»¹»ǿΒΡ»ΐΫ«–ΈΒΡΟφΜΐœύΒ»Θ©Θ§
Φ¥![]() Θ°
Θ°
Θ®3Θ©»γΆΦΘ§ΙΐΒψDΉς![]() ΫΜAB”Ύ
ΫΜAB”Ύ![]() Θ°
Θ°

ΓΏ![]() Θ§
Θ§
ΓύΥΡ±Ώ–Έ![]() «ΤΫ––ΥΡ±Ώ–ΈΘ§
«ΤΫ––ΥΡ±Ώ–ΈΘ§
ΓΏΓœABCΘΫ60ΓψΘ§BDΤΫΖ÷ΓœABCΘ§
Γύ![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύΥΡ±Ώ–Έ![]() «Νβ–ΈΘ§
«Νβ–ΈΘ§
Γύ![]() Θ§
Θ§
ΓΏBEΓΔ![]() …œΒΡΗΏœύΒ»Θ§
…œΒΡΗΏœύΒ»Θ§
Γύ![]() ,
,
ΓύΒψ![]() «Υυ«σΒΡΒψΘΜ
«Υυ«σΒΡΒψΘΜ
ΙΐΒψDΉς![]() Θ§
Θ§
ΓΏ![]() ,
,![]() Θ§
Θ§
Γύ![]()
ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ![]() «Β»±Ώ»ΐΫ«–ΈΘ§
«Β»±Ώ»ΐΫ«–ΈΘ§
Γύ![]() Θ§
Θ§
ΓΏBDΘΫCDΘ§
ΓύΓœDBCΘΫΓœDCBΘΫ30ΓψΘ§
Γύ![]()
Γύ![]() Θ§
Θ§
![]() ΘΫ360Γψ150Γψ60ΓψΘΫ150ΓψΘ§
ΘΫ360Γψ150Γψ60ΓψΘΫ150ΓψΘ§
Γύ![]() Θ§
Θ§
ΓΏ‘Ύ![]() ΚΆ
ΚΆ![]() ÷–Θ§
÷–Θ§

Γύ![]() Θ®SASΘ©Θ§
Θ®SASΘ©Θ§
Γύ![]()
ΓΏ![]() ,
,
Γύ![]()
ΓύΒψ![]() “≤ «Υυ«σΒΡΒψΘ§
“≤ «Υυ«σΒΡΒψΘ§
Γύ‘Ύ…δœΏBA…œ¥φ‘ΎΒψFΒΡΗω ΐ”–ΝΫΗω.